Grenzwert mit Sandwichsatz bestimmen

Question

Aufgabe:

Bestimmen Sie, z.B. mit Hilfe des Sandwichsatzes, die folgenden Grenzwerte:

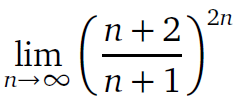
Text erkannt:

\( \lim \limits_{n \rightarrow \infty}\left(\frac{n+2}{n+1}\right)^{2 n} \)

Problem/Ansatz:

Hallo, irgendwie komme ich bei dieser Aufgabe nicht weiter. Es wäre mir sehr geholfen, wenn mir jemand erklären könnte wie ich folgenden Grenzwert bestimmen kann.

Ich hoffe ich habe alles richtig gepostet, da dies mein erster Eintrag hier im Forum ist. Danke für eure Hilfe.

Answer 1

\( \begin{aligned} \lim \limits_{n \rightarrow \infty}\left(\frac{n+2}{n+1}\right)^{2 n} &=\lim \limits_{n \rightarrow \infty}\left(\frac{n+1+1}{n+1}\right)^{2 n} \\ &=\lim \limits_{n \rightarrow \infty}\left(1+\frac{1}{n+1}\right)^{2 n} \\ &=\lim \limits_{n \rightarrow \infty}\left(1+\frac{1}{n+1}\right)^{2(n+1)}\left(1+\frac{1}{n+1}\right)^{-2} \\ &=\lim \limits_{n \rightarrow \infty}\left(\left(1+\frac{1}{n+1}\right)^{n+1}\right)^{2}\left(1+\frac{1}{n+1}\right)^{-2} \\ &=\lim \limits_{n \rightarrow \infty}\left(\left(1+\frac{1}{n+1}\right)^{n+1}\right)^{2} \lim \limits_{n \rightarrow \infty}\left(1+\frac{1}{n+1}\right)^{-2} \\ &=\left(\lim \limits_{n \rightarrow \infty}\left(1+\frac{1}{n+1}\right)^{n+1}\right)^{2}=e^{2} \end{aligned} \)

Verwendet wurde die Definition der Eulerschen Zahl, Reinziehen des Limes in stetige Funktionen, und Multiplikativität des Limes bei konvergenten Folgen.

Comments

Hätte man dies eigentlich mit Sandwich überhaupt lösen können?

---

Ja, aber dafür musst du natürlich erstmal wissen, dass es gegen e^2 konvergiert, um das dann mit dem Sandwich Theorem zu beweisen. Gerne die Antwort akzeptieren, wenn sie hilfreich war :D

---

Könntest du vielleicht noch kurz demonstrieren wie ich da jetzt weitermachen müsste. Also fürs Sandwich Theorem? Wär' wirklich super.

---

Du brauchst doch kein Sandwich theorem, das was ich oben hingeschrieben habe ist schon der Beweis. In der Aufgabe steht ja nur "z.B.", also ist nur eine Möglichkeit.

---

Achso das klang so als ob's nicht fertig wäre und ich war schon komplett verwirrt.

---

Vielen Dank dann!

---

Sandwich theorem wäre jetzt nur noch unnötiger zusätzlicher Rechenaufwand, bei dem du eben einfach beide Seiten abschätzt.

---

Also sowie es in der Antwort darüber steht mit dem Abschätzen...

Answer 2

Moinsen der Grenzwert ist e^2. Das heißt, nach oben hin solltest du erstmal den Bruch umschreiben zu (1+1/n+1) und dann n+1 durch n ersetzen. Nach unten solltest du den Bruch auch so umschreiben und n+1=m setzen und dann m entsprechend auch in den Exponenten schreiben. Dadurch steht dann dort, wenn du es auflöst (1+1/m)^(-2) und dann setzt du m-1 in den Nenner. Dann hast du deine Abschätzung nach unten und der Grenzwert geht auch gegen e^(-2)