Fallunterscheidung mit 2 Beträgen? Meine Ungleichung ist : |x-1|<|x-3|

Question

Meine Ungleichung ist : |x-1|<|x-3|

Wie komme ich jetzt auf die verschiedenen Fälle? Bitte mit Erklärung :-)

 

Answer 1

laut Wolfram Alpha gilt diese Ungleichung für alle x<2:

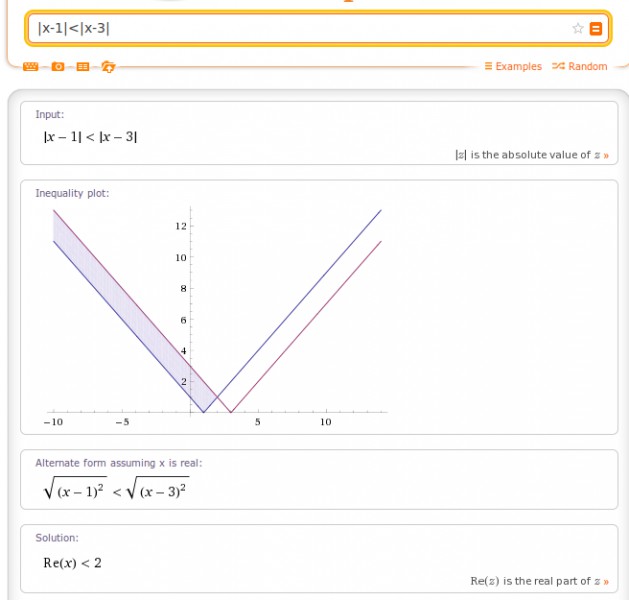
Da die Beträge in der Ursprungs-Ungleichung positiv sind, kann man beide Seiten quadrieren und erhält:

(x - 1)² < (x - 3)²

x² - 2x + 1 < x² - 6x + 9

-2x + 1 < -6x + 9 | +2x - 1

0 < -4x + 8 | +4x

4x < 8 | :4

x < 2

 

Fallunterscheidungen wären aufwändiger:

1. (x - 1) ≥ 0 und (x - 3) ≥ 0

2. (x - 1) ≥ 0 und (x - 3) < 0

3. (x - 1) < 0 und (x - 3) ≥ 0

4. (x - 1) < 0 und (x - 3) < 0

 

Besten Gruß

Comments

Alles klar! Danke  für eure schnellen Antworten, war völlig verwirrt(weil noch nie gemacht), da habe ich gar nicht so einfach gedacht ;-)

---

Gern geschehen!

Ich habe auch erst bei Wolfram Alpha kontrolliert, ob man es so einfach rechnen kann :-)

Answer 2

Du musst hier keine Fälle unterscheiden, wenn du auf beiden Seiten quadrierst. Grund (|a|)^2 = a^2.

|x-1|<|x-3|          |^2

x^2 - 2x + 1 < x^2 -6x + 9

 - 2x + 1 <  -6x + 9

4x < 8

x < 2

L = {x | x<2}

vgl. https://www.wolframalpha.com/input/?i=%7Cx-1%7C+%3C+%7Cx-3%7C