Hier der Graph der die hilft die Nullstellen
und die Funktion zu verstehen.
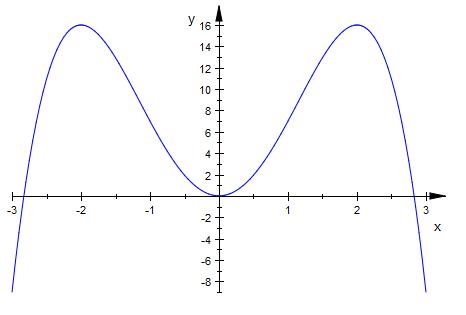
f ( x ) = 8 * x^2 - x^4
Stammfunktion
S ( x ) = 8 * x^3 / 3 - x^5 / 5
Die Funktion ist symmetrisch. Es genügt
S ( x ) zwischen 0 und 2 * √ 2
zu berechnen und dann " mal 2 " zu nehmen.
Bei Bedarf wieder melden.