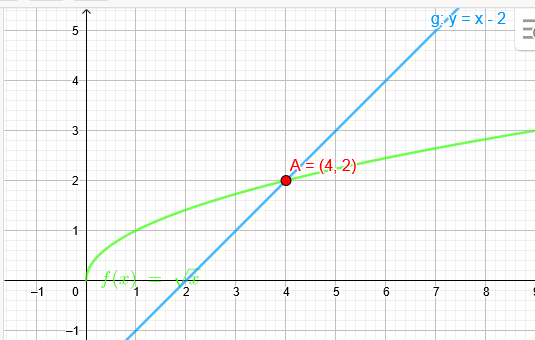
Man soll den Flächeninhalt des Teils bestimmen, welcher im ersten Quadranten \(y = \sqrt{x} \) und von unten durch die x Achse und die Gerade \(y = x-2\) begrenzt wird
Schnittpunkt von der Geraden mit: \(y = \sqrt{x} \) → \(x=4\)
\(d(x)= \sqrt{x}-(x-2)=\sqrt{x}-x+2\)
\( A=\int\limits_{0}^{4}(\sqrt{x}-x+2)*dx=\int\limits_{0}^{4}(x^{\frac{1}{2}}-x+2)*dx=... \)