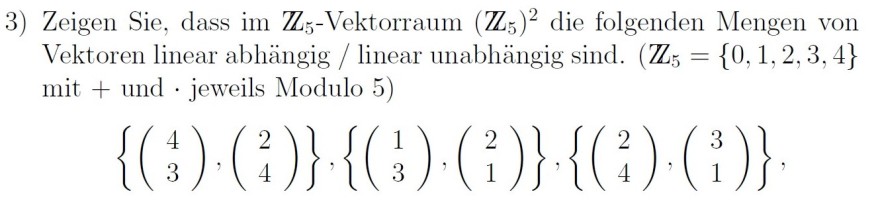
Text erkannt:
3) Zeigen Sie, dass im \( \mathbb{Z}_{5} \)-Vektorraum \( \left(\mathbb{Z}_{5}\right)^{2} \) die folgenden Mengen von Vektoren linear abhängig / linear unabhängig sind. \( \left(\mathbb{Z}_{5}=\{0,1,2,3,4\}\right. \) mit \( + \) und \( \cdot \) jeweils Modulo 5 )
\( \left\{\left(\begin{array}{l} 4 \\ 3 \end{array}\right),\left(\begin{array}{l} 2 \\ 4 \end{array}\right)\right\},\left\{\left(\begin{array}{l} 1 \\ 3 \end{array}\right),\left(\begin{array}{l} 2 \\ 1 \end{array}\right)\right\},\left\{\left(\begin{array}{l} 2 \\ 4 \end{array}\right),\left(\begin{array}{l} 3 \\ 1 \end{array}\right)\right\}, \)
Aufgabe:
Ich muss hier die lineare Abhängigkeit bzw. Unabhängigkeit bestimmen, wie man das mach weiß ich nur versteh ich nicht was mit dem Z5 gemeint ist und auch das modulo 5 versteh ich nicht.