Aufgabe:
beweis dafür das die innenwinkelsumme immer 180 grad ist?
Problem/Ansatz:
Hello liebe leute, ich hadere mit der ganz komischen aufgabe c. ich verstehe nicht ganz wie ich das zeigen soll. und zu erklärung, die in der aufgabe c) genannten a und 2.
in der aufgabe a wurde der stufenwinkelsatz beweisen
in der aufgabe 2 wurde die innenwinkel summe eines dreiecks bewiesen.
und jetzt stehe ich bei c aber total in einer sackgasse ich hoffe es kann mir einer weiterhelfen.
Text erkannt:
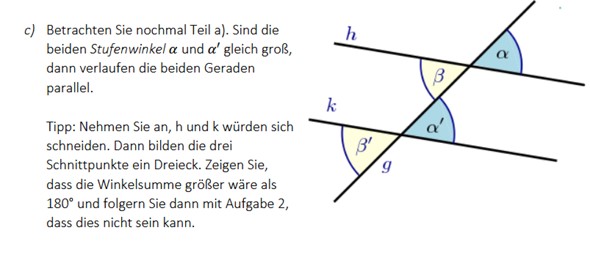
c) Betrachten Sie nochmal Teil a). Sind die beiden Stufenwinkel \( \alpha \) und \( \alpha^{\prime} \) gleich groß, dann verlaufen die beiden Geraden parallel.