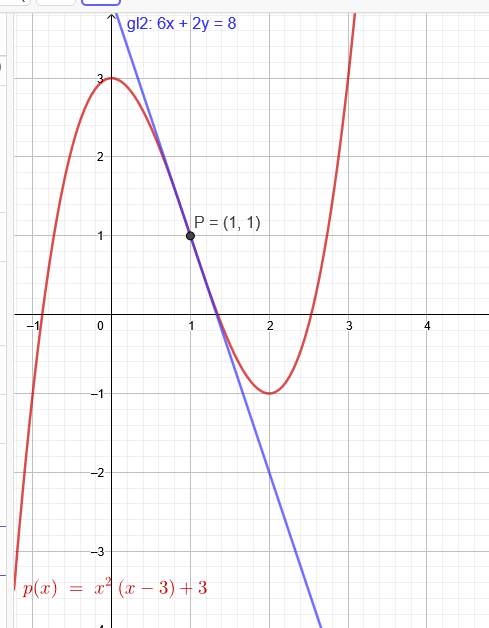
"Eine Polynomfunktion dritten Grades hat den Hochpunkt H(0|3). Die Tangente im Punkt P(1|yp) hat die Gleichung tp : 6x+2y = 8.
Bestimmen Sie den Funktionsterm der Polynomfunktion!"
P(1|1)→P´(1|-2)
H(0|3)→H´(0|0) doppelte Nullstelle:
\(f(x)=a*x^2*(x-N)\)
P´(1|-2):
\(f(1)=a*(1-N)→a*(1-N)=-2→a=\frac{2}{N-1}\)
\(tp : 6x+2y = 8→ y = 4-3x\) Steigung der Tangente in P(1|yp) ist m=-3
\(f(x)=\frac{2}{N-1}*x^3-\frac{2}{N-1}*x^2*N\)
\(f´(x)=3*\frac{2}{N-1}*x^2-2*\frac{2}{N-1}*x*N\)
\(f´(1)=3*\frac{2}{N-1}-2*\frac{2}{N-1}*N\)
\(3*\frac{2}{N-1}-2*\frac{2}{N-1}*N=-3\) → \(N=3\) →a=1\)
\(f(x)=x^2*(x-3)\)
\(p(x)=x^2*(x-3)+3\)
P ist somit auch Wendepunkt der Parabel.