Hallo,
du kennst die Koordinaten des Punktes und die 1. Ableitung = Steigung m der Tangente = 1
Eingesetzt in die allgemeine Geradengleichung y = mx + n mit n = Schnittpunkt der Geraden mit y-Achse
ergibt
-1 = 1·4 + n ⇒ n = -5
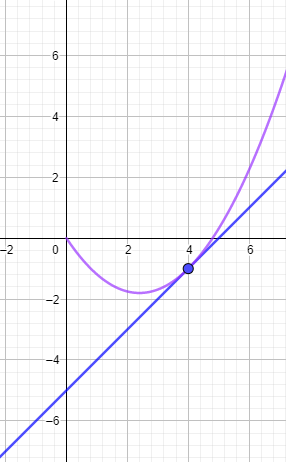
Jetzt kannst du die Gerade einzeichnen und eine passende Kurve dazu.
Gruß, Silvia