Bestimmen Sie, wie hoch das Brett über dem Boden ist.

Question

Aufgabe:

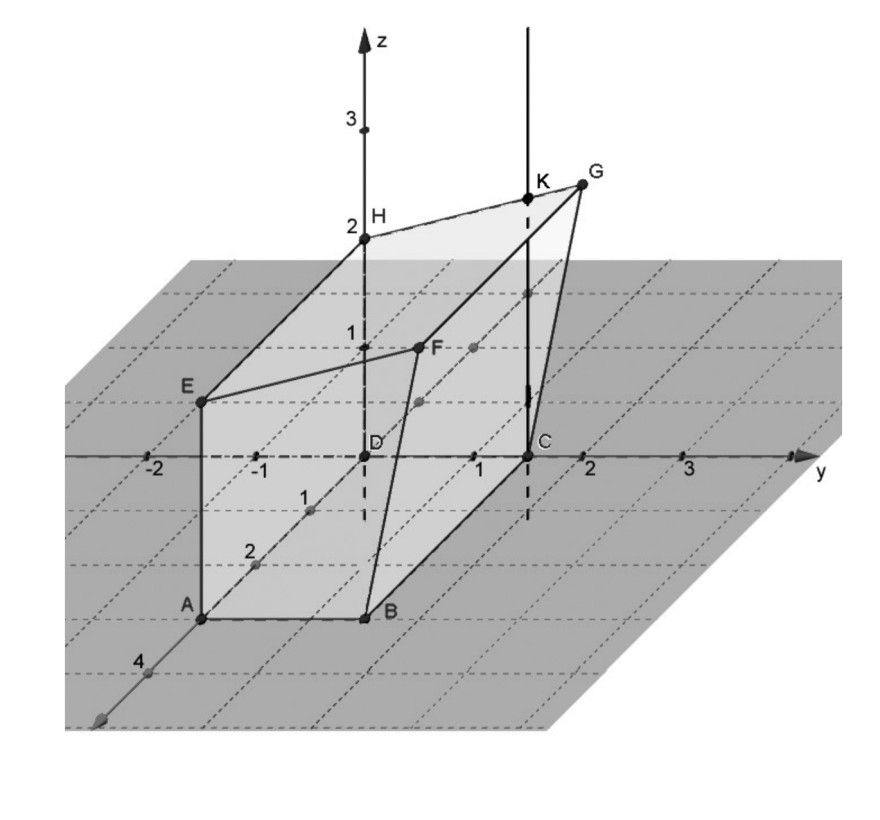
Für einen Stand am Wochenmarkt soll eine Hütte gebaut werden (siehe Material 1). Die Bodenfläche ist rechteckig, 3m lang und 1,5 m breit. Die Rückwand ist ebenfalls rechteckig und 2m hoch. Damit die Kunden vor Regen geschützt sind und das Wasser ablaufen kann, soll der Punkt G des rechteckigen Dachs in der Zeichnung bei (0I2I2,5) liegen (1 LE entspricht 1 m)

A (3I0I0)

B (3I1,5I0)

C (0I1,5I0)

D (0I0I0)

E (3I0I0)

F (3I2I2,5)

G (0I2I2,5)

H (0I0I2)

e) Zum Auslegen der Ware wird 30cm unterhalb der Mitte von CG ein Brett parallel zur Bodenfläche eingezogen. Bestimmen Sie, wie hoch das Brett über dem Boden ist.

f) Berechnen Sie das Volumen der Hütte, also des Körpers ABFEDCGH.

Tipp: Nutzen Sie DCGH als Grundfläche des Körpers

Problem/Ansatz:

1.) Hierfür, also für e), habe ich als erstes den Mittelpunkt zwischen C und G ermittelt M(0I1,75I2,5)

2.) Ich habe den Betrag des Mittelpunktes berechnet —>  ca. 2, 15 und davon 30 cm abgezogen —> 1, 85 m

Doch ich komme nicht weiter um weiß nicht welche Rechenschritte als nächstes folgen müssen, um die Höhe zu berechnen.

Answer 1

e) Zum Auslegen der Ware wird 30cm unterhalb der Mitte von CG ein Brett parallel zur Bodenfläche eingezogen. Bestimmen Sie, wie hoch das Brett über dem Boden ist.

Das Brett ist 1,25 - 0,3 m über dem Boden.

Comments

Könnten Sie mir vielleicht sagen, wie Sie auf diese Antwort gekommen sind?

---

Die Mitte von (a|b|c) und (d|e|f) ist (\( \frac{a+d}{2} \)|\( \frac{b+e}{2} \)|\( \frac{c+f}{2} \)).

Die z-Koordinate nennt die Höhe über dem Boden (x-y-Ebene).

---

1,25 kann gar nicht sein, das wäre die Höhe des Mittelpunktes. es muss 30cm darunter sein

---

Das habe ich tatsächlich nicht berücksictigt. Wurde korrigiert.