Aloha :)
Willkommen in der Mathelounge... \o/
1) Bestimmung der Extremwert-Kandidaten
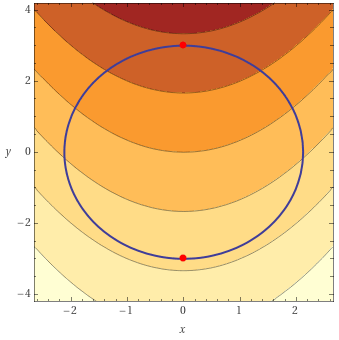
Wir sollen \(f(x;y)\) unter einer konstanten Nebenbedingung \(g(x;y)\) optimieren:$$f(x;y)=2x^2-6y\quad;\quad g(x;y)=2x^2+y^2-9=0$$
Nach Lagrange muss der Gradient der zu optimierenden Funktion eine Linearkombination der Gradienten aller Nebenbedingungen sein. Hier haben wir nur eine Nebenbedingung, also lautet die Forderung:$$\operatorname{grad}f(x;y)=\lambda\operatorname{grad}g(x;y)\implies\binom{4x}{-6}=\lambda\binom{4x}{2y}$$Das heißt, dass die beiden Gradienten kollinear sein müssen. Daher spannen sie keine Fläche auf und ihre Determinante muss verschwinden:$$0\stackrel!=\operatorname{det}\begin{pmatrix}4x & 4x\\-6 & 2y\end{pmatrix}=8xy-24x=8x(y-3)\quad\implies\quad x=0\;\lor\;y=3$$
Diese Lagrange-Bedingungen setzen wir in die Nebenbedingung ein:$$x=0\implies9=2x^2+y^2=y^2\implies y=\pm3\quad\implies\quad K_1(0|-3)\;;\;K_2(0|+3)$$$$y=3\implies9=2x^2+y^2=2x^2+9\implies x=0\quad\implies\quad\text{kein neuer Kandidat}$$Wir haben also zwei Kandidaten für Extremwerte gefunden.
2) Bewerten der Kandidaten
Die Funktionswerte bei den beiden Kandidaten \(K_1(0;-3)\) und \(K_2(0;3)\) lauten:$$f(0;-3)=18\quad;\quad f(0;3)=-18$$Für \(x=0\) verläuft \(f(0;y)=-6y\) linear. Daher ist \(K_1\) ein Maximum und \(K_2\) ein Minimum.