Signifikanzniveau nur aus n und p berechnen

Question

Aufgabe:

Eine Aussage lautet: "Von 100 Haustierbesitzern haben maximal 45% einen Hamster."

Wie groß ist die Wahrscheinlichkeit, dass die Aussage abgelehnt wird, obwohl sie richtig ist?

Problem/Ansatz:

Gesucht ist wohl das Signifikanzniveau. Fehler 1. und 2. Art sind klar, aber wie komme ich mit den wenigen Angaben zu einer Lösung? Eine F-Tabelle für die Werte habe ich, aber wie kann ich den kritischen Wert berechnen, ab dem die Aussage angenommen bzw. abgelehnt wird?

Answer 1

Wie groß ist die Wahrscheinlichkeit, dass die Aussage abgelehnt wird, obwohl sie richtig ist?

Ohne eine Angabe der Entscheidungsregel ist die Beantwortung der Frage nicht möglich.

Halte also ausschau in der Aufgabe nach eine Angabe wann die Nullhypothese angenommen/abgelehnt wird.

Comments

In der Aufgabe steht nur noch, dass ein Testverfahren bestimmt werden soll, mit dem man die Aussage überprüfen kann. Dann soll berechnet werden, wie groß die Wahrscheinlichkeit ist, dass die Aussage abgelehnt wird, obwohl sie richtig ist.

---

Ok. Dann darfst du dir ein Signifikanzniveau aussuchen. Beliebt ist ein 5% Signifikanzniveau.

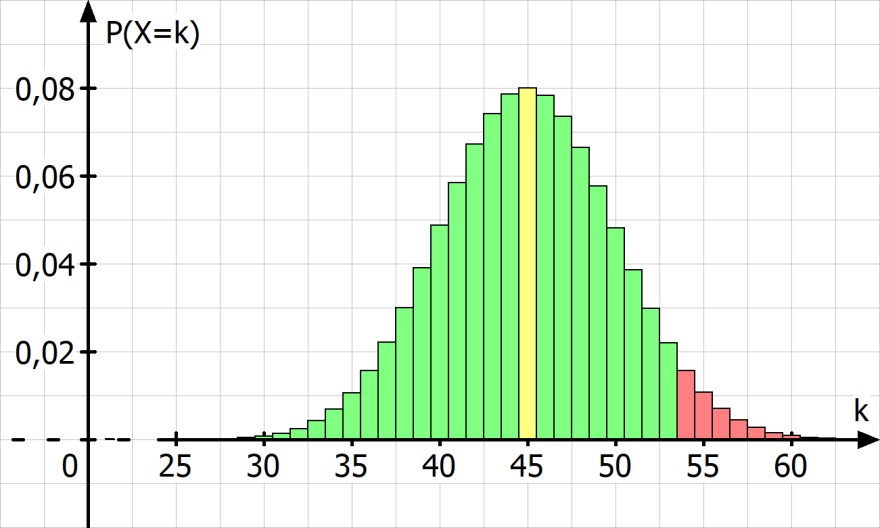
Annahme der Nullhypothese im Intervall {0,...,53}

Ablehnung der Nullhypothese im Intervall {54,...,100}

Der Fehler erster Art beträgt hier P(X >= 54) = 4.41%

Um den Fehler zweiter Art zu bestimmen bräuchtest du eine abweichende Wahrscheinlichkeit. Also z.B. 50%

---

Danke, dann habe ich tatsächlich alles richtig gemacht!

Für den Fehler 2. Art ist p = 0,6.