Aufgabe:

Text erkannt:
b) Ein oben offener rechteckiger Behälter soll das Volumen \( V=10000 \mathrm{~cm}^{3} \) Haben. Bestimmen Sie mit der Langrange-Methode die Seitenlängen x,y,z so, dass die Oberfläche und somit der Materialverbrauch für den Behälter minimal wird. Den Nachweis des Minimums müssen Sie nicht erbringen
Problem/Ansatz:
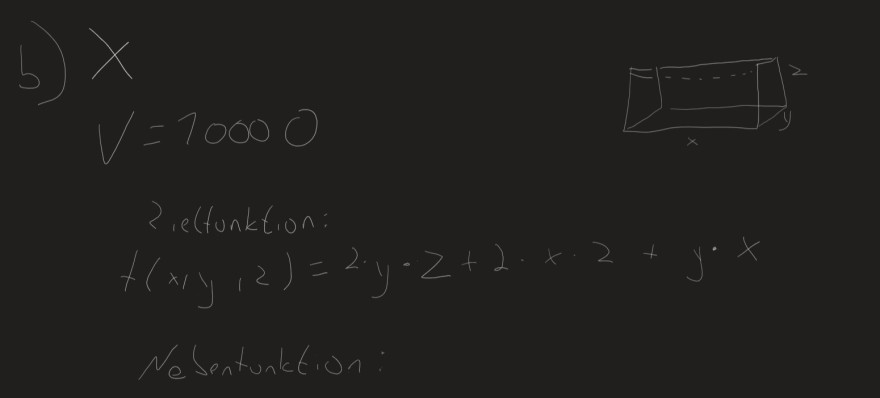
Text erkannt:
2eltunktion:
\( f(x, y, 2)=2 \cdot y \cdot z+2 \cdot x \cdot 2+y \cdot x \)
Nesentunktion:

Text erkannt:
\( g(x, y, 2)=x y \cdot 2-70000=0 \)

Text erkannt:
\( L(x, y, 21 / 1)=2 \cdot y \cdot 2+2 \cdot x \cdot 2+y \cdot x+\lambda(x \cdot y \cdot 2-10000)=0 \)
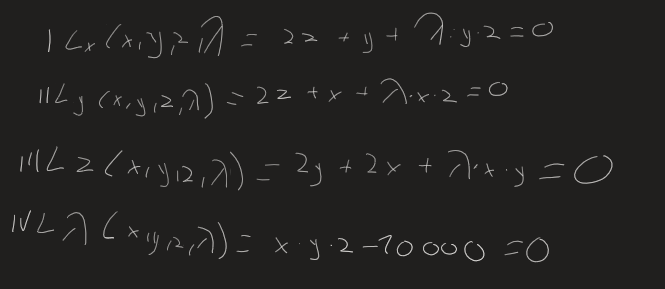
Text erkannt:
\( 1 L_{x}(x, y, 2 \lambda=22+y+\lambda \cdot y \cdot 2=0 \)
\( 11 L_{y}(x, y, 2, \lambda)=2 z+x+\lambda \cdot x \cdot 2=0 \)
\( 11 L z(x, y, 2, \lambda)=2 y+2 x+\lambda \cdot x \cdot y=O \)
\( 1 V L \lambda((x, y, 2, \lambda)=x \cdot y \cdot 2-10000=0 \)
Eigentlich muss ich hier nur noch die Variablen lösen, aber ich komme auf keinen richtigen Ansatz