Aufgabe: Bestimmen Sie das Volumen des folgenden Körpers.
Problem/Ansatz: In den Musterlösungen sind zwei Dinge,die ich nicht verstehe:
1.Warum ist r0 =\( \sqrt{z0} \) -z02 der Radius der Kreise
2. Warum ist x2 + y2 =\( \sqrt{z0} \) -z02 ein Kreis um den Punkt (0/0) ? 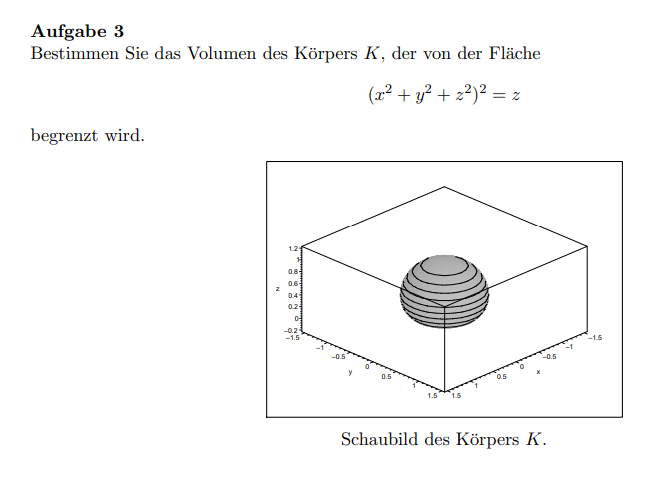
Text erkannt:
Aufgabe 3
Bestimmen Sie das Volumen des Körpers \( K \), der von der Fläche
\( \left(x^{2}+y^{2}+z^{2}\right)^{2}=z \)
begrenzt wird.
Schaubild des Körpers \( K \).

Text erkannt:
Lösung:
Der Körper \( K \) liegt zwischen den beiden Ebenen \( z=0 \) und \( z=1 \). Der Schnitt der Berandung des Körpers \( K \) mit der Ebene \( z=z_{0}, z_{0} \in[0,1] \), lautet
\( \begin{array}{r} \left(x^{2}+y^{2}+z_{0}^{2}\right)^{2}=z_{0} \Longleftrightarrow x^{2}+y^{2}+z_{0}^{2}=+\sqrt{z_{0}} \Longleftrightarrow x^{2}+y^{2}=\sqrt{z_{0}}-z_{0}^{2} . \\ \text { Dies ist ein Kreis um den Punkt } \left.(0,0) \text { vom Radius } r_{0}=\sqrt{\sqrt{z_{0}}-z_{0}^{2}}\right) \text { mit Flächeninhalt } \\ F\left(z_{0}\right)=\pi \cdot r_{0}^{2}=\pi \cdot\left(\sqrt{z_{0}}-z_{0}^{2}\right) . \end{array} \)
Damit gilt mit dem Prinzip von Cavalieri
\( \operatorname{Vol}(K)=\int \limits_{0}^{1} F(z) d z=\int \limits_{0}^{1} \pi \cdot\left(\sqrt{z}-z^{2}\right) d z=\pi \cdot\left[\frac{2}{3} \cdot z^{\frac{3}{2}}-\frac{z^{3}}{3}\right]_{z=0}^{1}=\frac{\pi}{3} \)