Wie untersuche ich die Funktion f(x) = x+1/x auf Monotonie?

Question

zb f(x) = x^5 + x^3

da ist die f'(x) ) 5x^4 + 3x^2,

da es hoch4 bzw. hoch 2 ist, also gerade, ist f'(x) größer gleich 0, also ist f(x) steigend

was ist zb mit f(x) = x+1/x Definitionsbereich: x>0

da ist die ableitung f'(x) = 1-1/x^2

wie mache ich da weiter?

Answer 1

Hi,

für die Monotonie gilt: f'(x)>0 (monoton steigend) oder f'(x)<0 (monoton fallend)

Für das erste Beispiel hast Du als recht. Es ist überall monoton steigend.

(Es wäre auch streng monoton steigend, wenn f'(x)≥0 gelten würde. Tut es aber nicht, da f'(0)=0 )


Für das zweite Beispiel hast Du

g(x) = x + 1/x

g'(x) = 1-1/x^2


Finde die Nullstellen:

g'(x) = 1-1/x^2 = 0

1 = 1/x^2

x^2 = 1

x = ±1


Jetzt nur noch bestimmen, für welche Intervalle g'(x)>0 oder  g'(x)<0 ist. Punktprobe mit x = 0,5

g'(0,5) = -3

Folglich liegt steigende Monotonie in den Intervallen x∈(-∞;-1) und x∈(1;∞) vor.

Fallende Monotonie dazischen: x∈(-1;1)

(Definitionsbereich noch beachten)


Grüße

Comments

Gerne :)    .

Answer 2

 

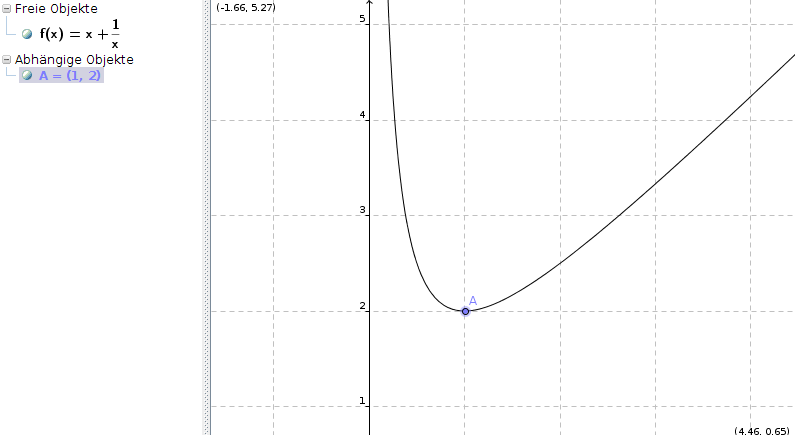
f(x) = x + 1/x

f'(x) = 1 - 1/x²

Offensichtlich ist x = 1 ein Kandidat für eine Extremstelle. Deshalb würde ich f''(x) bilden:

f''(x) = 2/x³

f''(1) = 2 > 0, also liegt an der Stelle x₀ = 2 ein lokales Minimum vor.

Nun einen Wert 0 < x < 1 in f'(x) einsetzen, z.B. x = 0,5

f'(0,5) = 1 - 1/0,25 = 1 - 4 = -3 < 0, also monoton fallend.

Und einen Wert x > 1, zum Beispiel x = 2

f'(2) = 1 - 1/4 = 3/4 > 0, also monoton steigend.

Vielleicht ist Dir das eine kleine Hilfe :-)

 

 

Besten Gruß

Comments

Auch ein gute Alternative. Verstehe aber eines nicht.

Nun einen Wert 0 < x < 1 in f'(x) einsetzen, z.B. x = 0,5

Wie kommst Du auf die untere Grenze?

---

@Unknown:

Der Fragesteller hat angegeben:

"Definitionsbereich: x>0"

---

Ach das hatte ich in der Eile als x≠0 gelesen :D.

Danke fürs auf die Finger hauen, wegen ungenau lesen :D.

---

@Unknown:

Wer haut denn hier auf die Finger?

Ich nicht :-D