Guten Morgen, können Sie mir bitte Aufgabe 1 Jacobi-Matrix von f erklären? Ich weiß, wie man Jacobi-Matrix rechnet aber diese Aufgabe hat mich fertig gemacht. Ich verstehe nicht, wie man auf x/(die Wurzel von 1-r^2)^3 kommt! Und wie rechnet man hier überhaupt die Ableitung, dass man hier 3×3 Spalten hat.
Bitte helfen Sie mir weiter!!!

Text erkannt:
Aufgabe A.11.1 (Jacobi-Matrizen)
Gegeben seien die Funktionen \( f: D \rightarrow \mathbb{R}^{3}, g: \mathbb{R}^{2} \rightarrow \mathbb{R}^{3} \) mit
\( \begin{array}{l} f(x, y, z)=\frac{1}{\sqrt{1-r^{2}}}(x, y, z)^{T} \text { mit } D:=\left\{(x, y, z)^{T} \mid r=\sqrt{x^{2}+y^{2}+z^{2}}<1\right\} \subset \mathbb{R}^{3}, \\ g(u, v)=\left(\frac{1}{\sqrt{2}} e^{u} \sin v, \frac{1}{\sqrt{2}} e^{u} \cos v, u v\right)^{T} . \end{array} \)
Bestimmen Sie die Jacobi-Matrizen von \( f \) und \( g \) an einer beliebigen Stelle. Berechnen Sie außerdem die Jacobi-Matrix von \( f \circ g \) an der Stelle \( \left(0, \frac{\pi}{4}\right)^{T} \).
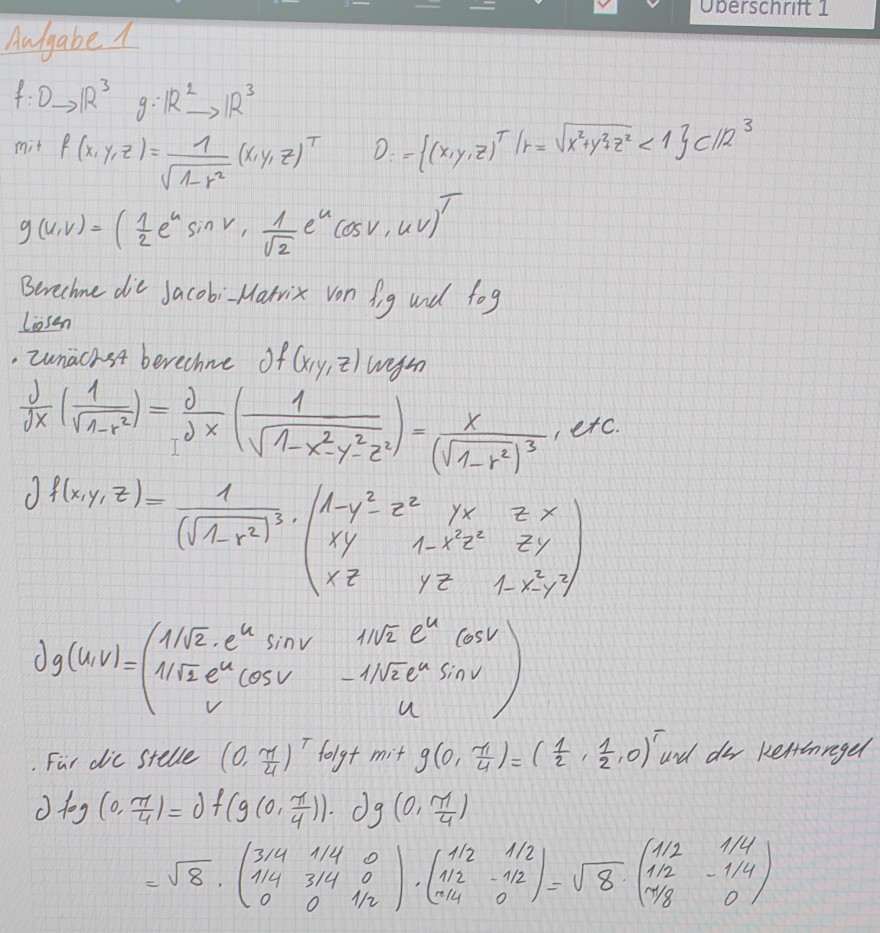
Text erkannt:
\( f: D \rightarrow \mathbb{R}^{3} \quad g: \mathbb{R}^{2} \rightarrow \mathbb{R}^{3} \)
mit \( f(x, y, z)=\frac{1}{\sqrt{1-r^{2}}}(x, y, z)^{\top} \quad D=\left\{(x, y, z)^{\top} \mid r=\sqrt{x^{2}+y^{2} z z^{2}}<1\right\} \subset \mathbb{R} \mathbb{R}^{3} \)
\( g(u, v)=\left(\frac{1}{2} e^{u} \sin v, \frac{1}{\sqrt{2}} e^{u} \cos v, u v\right)^{\top} \)
Berchure die Jacobi-Matrix von fig und fog
- zunachst berechne of \( (x, y, z) \) weym
\( \frac{\partial}{\partial x}\left(\frac{1}{\sqrt{1-r^{2}}}\right)=\frac{\partial}{\partial x}\left(\frac{1}{\sqrt{1-x^{2}-y^{2}-z^{2}}}\right)=\frac{x}{\left(\sqrt{1-r^{2}}\right)^{3}} \), etc.
\( \partial f(x, y, z)=\frac{1}{\left(\sqrt{1-r^{2}}\right)^{3}} \cdot\left(\begin{array}{ccc}1-y^{2}-z^{2} & y x & z x \\ x y & 1-x^{2} z^{2} & z y \\ x z & y z & 1-x^{2} y^{2}\end{array}\right) \)
\( \operatorname{dg}(u, v)=\left(\begin{array}{cc}1 / \sqrt{2} \cdot e^{u} \sin v & 1 / \sqrt{2} e^{u} \cos v \\ 1 / \sqrt{2} e^{u} \cos v & -1 / \sqrt{2} e^{u} \sin v \\ v & u\end{array}\right) \)
Fur dic stelle \( \left(0, \frac{\pi}{4}\right)^{\top} \) folgt mit \( g\left(0, \frac{\pi}{4}\right)=\left(\frac{1}{2}, \frac{1}{2}, 0\right)^{\top} \) und der kettennged
\( \partial \log \left(0, \frac{\pi}{4}\right)=\partial f\left(g\left(0, \frac{\pi}{4}\right)\right) \cdot \partial g\left(0, \frac{\pi}{4}\right) \)
\( =\sqrt{8} \cdot\left(\begin{array}{ccc}3 / 4 & 1 / 4 & 0 \\ 1 / 4 & 3 / 4 & 0 \\ 0 & 0 & 1 / 2\end{array}\right) \cdot\left(\begin{array}{cc}1 / 2 & 1 / 2 \\ 1 / 2 & -1 / 2 \\ 1 / 4 & 0\end{array}\right)=\sqrt{8} \cdot\left(\begin{array}{cc}1 / 2 & 1 / 4 \\ 1 / 2 & -1 / 4 \\ \pi / 8 & 0\end{array}\right) \)