Oberfläche Rotationskörper nach der Guldin-Regel

Question

Text erkannt:

Dargestellt ist ein Erdwall, der zu Schallschutzzwecken als Rotationskörper (zur Achse I-I) in einem Kreisausschnitt mit dem Winkel \( \rho \) um eine Wohnsiedlung herum angeschüttet wird.
Ermitteln Sie die Oberfläche des Dammes, die zur Bepflanzung vorgesehen ist.
\( O_{\text {Damm }}= \)
\( m^{2} \)

Aufgabe:

Berechnen Sie die Oberfläche Rotationskörper nach der Guldin-Regel.

Comments

Hallo

die Guldini Regel steht aber nicht im Originaltext, den du gepostet hast. also was genau ist die Aufgabe?

aber da du ja nur gerade Strecken hast wo deren Schwerpunkt in der Mitte liegt, rechne die Kegelstümpfe einfach so aus. Das ist dann wohl die Regel für Oberflächen.

lul

Answer 1

Du brauchst für die Berechnung die Schwerpunktkoordinaten des Trapez. Die berechnen sich folgendermaßen

Zum Schwerpunkt bei der x-Achse musst Du noch den Abstand \( e = 329 \) Meter dazu addieren. Ich habe dann folgende Koordinaten für den Schwerpunkt

\( x_S = 339.372 \)  und \( y_S = 1.912 \)

Die Mantelfläche ergibt sich aus der Berechnung zweier Kegelstümpfe. Dazu musst Du die Länge der äußeren und inneren Begrenzungslinien berechnen sowie die Abstände deren Schwerpunkte zur Rotationsachse.

Bei einem Kegelstumpf der so aus sieht

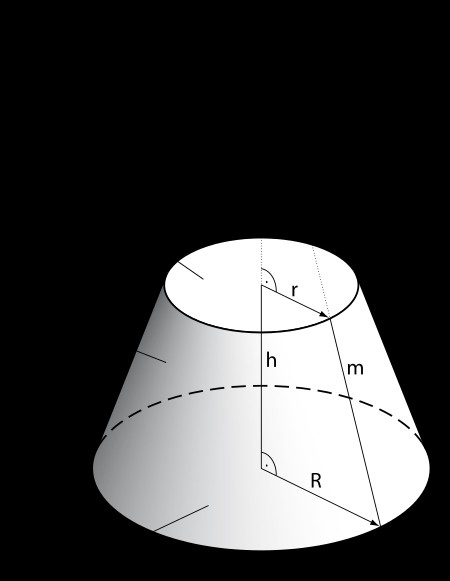
kommt man über die Guldinsche Formel zu folgender Mantelfläche

$$ M = m \cdot \pi \cdot 2 \left( r+ \frac{R - r}{2} \right) = m \cdot \pi \cdot (r+R) $$

Das musst Du jetzt für die beiden sich ergebenden Kegelstümpfe machen.

Answer 2

Hallo

die Guldiniregel ist für Volumen nicht für Oberflächen, wie in deiner vorigen Aufgabe bestimmst du die Oberfläche der 2 entstehenden Kegelstümpfe und des oberen Kreisring, von der Summe dann 127/360  weil es nur der Bruchteil des Ganzen ist.

Gruß lul

Comments

Danke für deine Antwort. Ich bekomme die Oberflächen leider nicht berechnet.

---

Ich muss wiedersprechen. Die Guldinsche Regel gilt auch für Mantelflächen Berechnungen und nicht nur für Volumen Berechnungen.

---

Sorry ullim hat recht, dann brauchst du doch nur den Schwerpunkt der Linien? Woran genau scheiterst du? lies die Regel notfalls in wiki nach   https://de.wikipedia.org/wiki/Rotationskörper

lul