Hallo,
In Richtung des Vektors (-1|-3|1) fällt paralleles Licht.
Da die Z-Koordinate \(z=1\gt 0\) ist, 'fällt' das Licht von unten nach oben; wenn ich mal unterstelle, dass \(+z\) 'oben' ist. Ist das richtig? Dann kann der senkrechte Stab aber keinen Schatten auf die xy-Ebene werfen!
Der Spurpunkt \(S_{xy} = (7|\,15|\, 0)\) ist dann aber korrekt. So sieht das aus
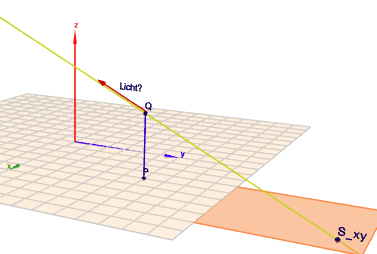
(klick auf das Bild!)
Zeichnerisch kommst Du über ein Schrägbild zum Ergebnis. Ich nehme an, Du weißt, wie man einen beliebigen Punkt mit bekannten Koordinaten in ein Schrägbild einzeichnet.
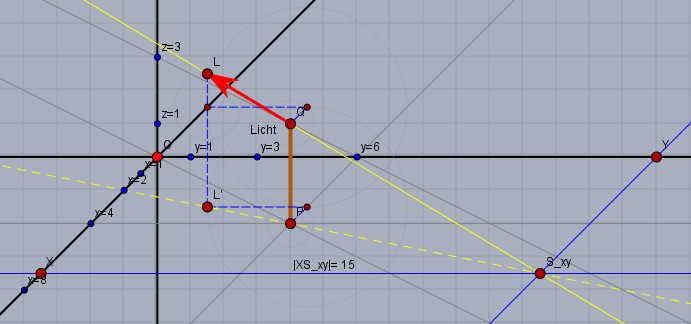
Dann zeichne zunächst die Punkte \(P\) und \(Q\) ein. Nun addiere den Lichtvektor zu \(Q\), der resultierende Punkt sei \(L\) und den zeichne auch ein. Die Gerade durch \(Q\) und \(L\) (gelb) ist der Lichtstrahl durch \(Q\).
Im Fußpunkt von \(Q\), das ist hier \(P\), zeichnest Du nochmal den Lichtvektor ein, aber nur mit seinen \(x\)- und \(y\)-Koordinaten. So kommst Du zu \(L'\). Die Gerade durch \(L'\) und \(P\) (gelb gestrichelt) ist die Spurgerade des Lichtstrahls durch \(Q\) in der XY-Ebene. Die Spurgerade schneidet den Lichtstrahl dann in \(S_{xy}\).
Nun kann man noch die Kordinaten ablesen. Die Y-Koordinate ist direkt messbar. Für die X-Koordinate muss man sich an der Skalierung der X-Achse orientieren, da diese die Schrägachse ist.
Falls Du noch Fragen hast, so melde Dich bitte.
Gruß Werner