Schattenbild eines Rechtecks

Question

Aufgabe:

Gegeben ist ein Rechteck ABCD mit A(4/3/0), B(2/3/0), C(2/3/3), D(4/3/3). Konstruieren Sie das Schattenbild des Rechtecks auf dem Boden und den Randflächen des 1. Oktanden. (sowohl gezeichnet, als auch gerechnet)

Problem/Ansatz:

Meine Idee wäre es jetzt erstmal die Spurpunkte zu berechnen. Muss ich dafür zwei Geradengleichungen aufstellen? Und wenn ja müssen das die Geradengleichungen AB & CD sein?

Comments

Dann sollte man auch informiert werden aus welcher Richtung das Licht kommt - weil ohne Licht kein Schatten...

---

Dann sollte man auch informiert werden aus welcher Richtung das Licht kommt -

Das Licht kommt auch hier wieder von unten! -> \((-1|\,-3|\,1)\)

---

Ja mei, es soll ja auch Bodenstrahler geben ;-)

---

Ah super danke. Wären die Geradengleichungen dann:

g_AB\( \vec{x} \)= \( \begin{pmatrix} 4\\3\\0 \end{pmatrix} \) + r \( \begin{pmatrix} -1\\-3\\1 \end{pmatrix} \)

& h_CD\( \vec{x} \)= \( \begin{pmatrix} 2\\3\\3 \end{pmatrix} \) + r \( \begin{pmatrix} -1\\-3\\1 \end{pmatrix} \) ?

---

Yep, und dann sollte y=0 sein, damit auf dieser Ebene was zu sehen ist...

---

Ja mei, es soll ja auch Bodenstrahler geben ;-)

schon recht! ... und Glasböden, damit man den Strahler so weit entfernt stellen kann, dass man mit parallelem Licht rechnen darf. Bleibt nur noch das große Geheimnis zu klären, warum ausgerechnet hinter dem Rechteck, das Bodenglas nicht mehr durchsichtig ist!? (siehe Bild am Ende der Frage).

Von den sonstigen Fehlern in diesem Bild ganz zu schweigen.

@breadsheep: wie heißt das Buch genau, aus dem Du diese Aufgabe hast?

---

Super, danke. Ich glaube ich habe es raus ich habe jetzt alle Spurpunkte berechnet. Also je 3 pro Gleichung & in das Koordinatensystem habe ich diese jetzt eingetragen + die Punkte A,B,C,D

---

@Werner-Salomon Die Aufgabe ist aus dem Buch "Mathematik Gymnasiale Oberstufe Nordrhein-Westfalen Qualifikationsphase Grundkurs" von Cornelsen.

---

Danke!               .

Answer 1

Um die Frage abzuschließen.

Es geht ja darum eine Gerade ausgehend von verschiedenen Punkten X mit einer Ebene zu schneiden:

n (X + t v) = d → t = (d - n X )/(n v) → t ∈ X + t v → X + (d - n X )/(n v) v }

wenn man jetzt aus den Schnittpunkten eine Matrix PPv baut

v=(-1,-3,1), n=(0,1,0), d=0 und  X=(x1,x2,x3)

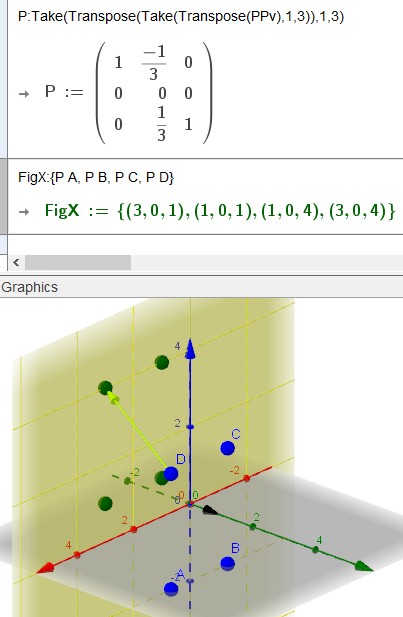
FigX sind die Bildkoordinaten in der Ebene y=0.

Du kannst natürlich jede der 4 Geraden ausgehend von A,B,C,D Richtung v einzeln abhandeln:

y Koordinaten 0 setzten -> t ausrechnen -> in Gerade einsetzen -> Bildpunkt