Aufgabe 1: Die Abbildung zeigt eine Brückenkonstruktion. Der Brückenbogen hat die Form einer Parabel.
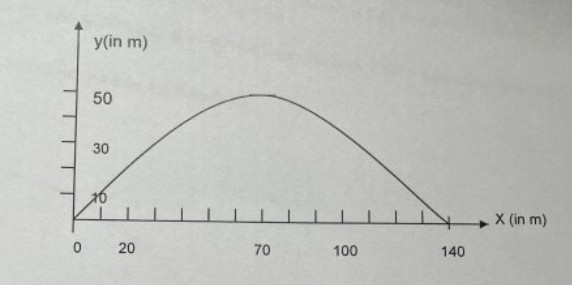
a) Gib die Spannweite der Brücke in Metern an.
b) Welche maximale Höhe hat die Brücke?
c) Eine der folgenden Funktionsgleichungen gehört zu der oben dargestellten Parabel. Kreuze an.
(1) \( f(x)=0,01 x+50 \)
(2) \( f(x)=0,01 x^{2}+50 \)
(3) \( f(x)=-0,01 x^{2}+1,4 x \)
d) Begründe, warum die beiden anderen Funktionsgleichungen aus Aufgabenteil c) nicht zu der oben abgebildeten Parabel gehören.
e) Berechne die Höhe des Brückenbogens für \( x=30 \mathrm{~m} \).
f) Ein anderer Stahlbrückenbogen kann durch die Gleichung \( g(x)=-0,02 x^{2}+1,8 x \) beschrieben werden.
f1) Welche Höhe hat diese Brücke bei \( x=25 \mathrm{~m} \) ?
f2) Berechne die Spannweite und die maximale Höhe dieser Brücke.
Aufgabe 2:
Auf Autobahnen kommt es bei schweren Unfällen oftmals zu einer Vollsperrung. Es entsteht ein Stau. Die Auflösung dieses Staus kann (vereinfacht) mit Hilfe einer Funktion \( f(x)=a x^{2}+c \) beschrieben werden. Der Faktor a hängt unter anderem davon ab, wie viele Fahrspuren nach Beseitigung der Unfallfolgen frelgegeben werden, \( c \) ist die maximale Staulänge.
In der Grafik wird die Auflösung eines \( 12,5 \mathrm{~km} \)-langen Staus nach der Freigabe von einer Fahrspur dargestellt.
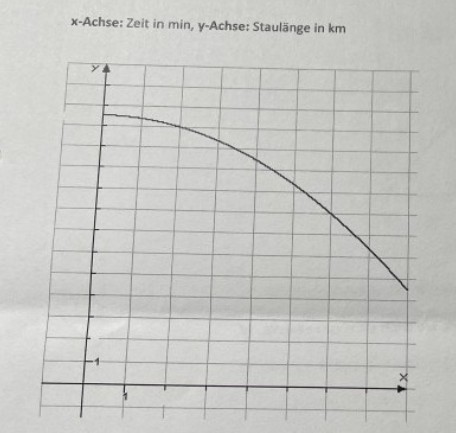
\( x \)-Achse: Zeit in min, \( y \)-Achse: Staulänge in \( \mathrm{km} \)
a) Wie lang ist der Stau nach 2 Minuten?
b) Nach wie vielen Minuten hat der Stau eine Länge von \( 8 \mathrm{~km} \) ?
c) Bestimme für die Funktion \( f(x) \) einen geeigneten Funktionsterm.
(Kontrollergebnis \( \left.f(x)=-0,125 x^{2}+12,5\right) \)
d) Berechne die Staulänge für den Zeitpunkt : „9 Minuten nach Aufhebung der Vollsperrung" .
e) Wie lange dauert es, bis der Stau sich vollständig aufgelöst hat?
f) Der Faktor a hat einen anderen Wert, wenn zwei Fahrspuren freigegeben werden.
f1) Skizziere in obigem Diagramm einen möglichen Graphen für diesen Fall. Begründe den Verlauf des Graphen.
f2) Gib einen möglichen Wert für a an.