Es gilt f(-1)=-1 und f(2)=8. Die Steigung der Sekante berechnet man wie folgt:
$$\dfrac{\text{Differenz der y Werte}}{\text{Differenz der x Werte}}=\dfrac{8-(-1)}{2-(-1)}=3$$
Wir suchen, also alle Stellen an denen die Steigung genau 3 ist. Dafür leiten wir ab: f'(x)=3x^2, setzen ein und lösen nach x auf:
$$f'(x)=3\Rightarrow 3x^2=3\Rightarrow x^2=1\Rightarrow x = 1\lor x=-1$$
Die beiden gesuchten Stellen sind also 1 und -1.
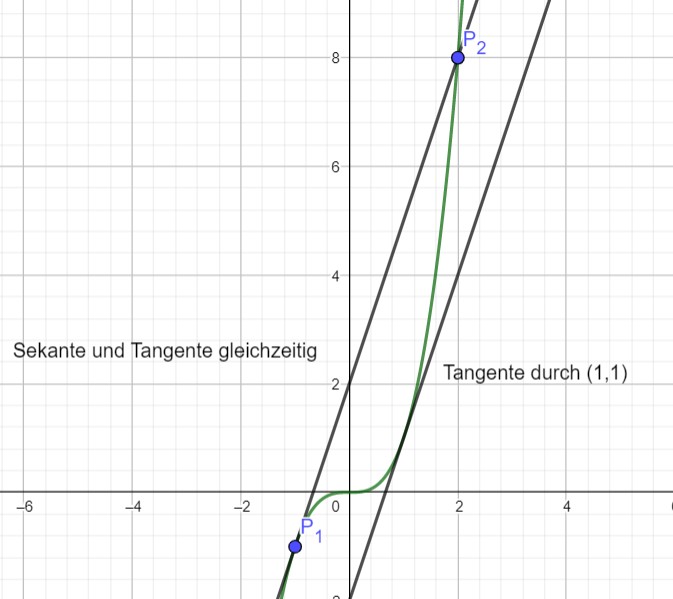
Skizze (man beachte, dass die Sekante und die Tangente durch (-1,-1) die gleiche Gerade sind):