Aufgabe:
Bestimme die Funktionsgleichungen aus den gegebenen Informationen. Arbeitsblatt von: Lektion F05: Gleichung einer Linearen Funktion bestimmen
Problem/Ansatz:
Funktion in Lösung ungleich in Aufgabenstellung?
Die Funktion in der Lösung ist mit (2|5) jedoch in Aufgabe (2|4) oder mache ich einen Denkfehler?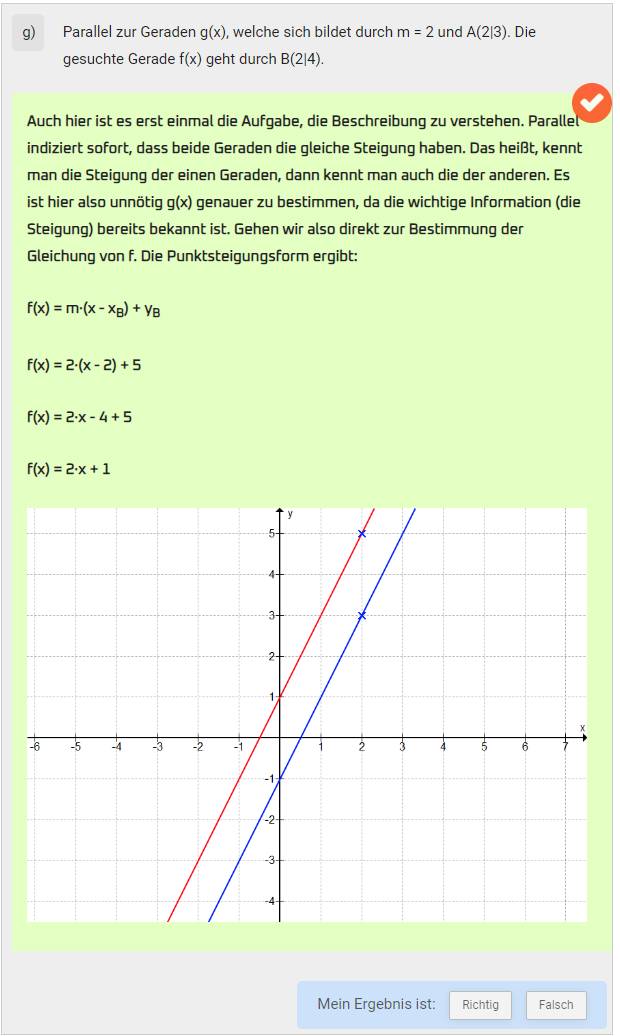
Text erkannt:
g) Parallel zur Geraden \( g(x) \), welche sich bildet durch \( m=2 \) und \( A(2 \mid 3) \). Die gesuchte Gerade \( f(x) \) geht durch \( B(2 \mid 4) \).
Auch hier ist es erst einmal die Aufgabe, die Beschreibung zu verstehen. Parallel indiziert sofort, dass beide Geraden die gleiche steigung haben. Das heißt, kennt man die Steigung der einen Geraden, dann kennt man auch die der anderen. Es ist hier also unnötig \( g(x) \) genauer zu bestimmen, da die wichtige Information (die Steigung) bereits bekannt ist. Gehen wir also direkt zur Bestimmung der Gleichung von f. Die Punktsteigungsform ergibt:
\( f(x)=m \cdot\left(x-x_{B}\right)+y_{B} \)
\( f(x)=2 \cdot(x-2)+5 \)
\( f(x)=2 \cdot x-4+5 \)
\( f(x)=2 \cdot x+1 \)
Mein Ergebnis ist:
Richtig
Falsch