Faires Spiel mit zwei Würfeln

Question

Aufgabe:

Betrachten Sie folgendes Spiel: Ein Spieler wählt zwei verschiedene Zahlen zwischen 1 und 6 und wirft 2 Würfel. Zeigen beide Würfel die genannten Zahlen an, erhält er 3 Euro. Ist unter den zwei Würfel genau eine genannte Zahl, erhält er 0.5 Euro. Wenn kein Würfel seine Zahlen anzeigt, muss der Spieler einen Euro zahlen.

a) Berechnen Sie den erwarteten Gewinn des Spielers.

b) Wie viel müsste der Spieler im Fall erhalten, dass beide Würfel seine Zahlen zeigen, damit es ein faires Spiel wäre?

Problem/Ansatz:

ich habe berechnet:

bei Punkt a) (1/6) hoch 2 * 3 + (1/6) hoch 2* 5/6 *0,5+ 1/6 * 5/6 hoch 2 *(-1)

aber Punkt b) kann nicht berechnen. wie geht es weiter?

Vielen Dank im Voraus!

Answer 1

Hallo,

eine Tabelle könnte erhellend wirken.

	Gewinn1	Gewinn2	Niete	Niete	Niete	Niete
Gewinn1	0,5€	3€	0,5€	0,5€	0,5€	0,5€
Gewinn2	3€	0,5€	0,5€	0,5€	0,5€	0,5€
Niete	0,5€	0,5€
Niete	0,5€	0,5€
Niete	0,5€	0,5€
Niete	0,5€	0,5€

Ich nehme dabei an, dass es nur 0,5€ gibt, wenn beide Würfel die gleiche Gewinnzahl anzeigen.

Die leeren Felder bedeuten, dass 1€ gezahlt werden muss.

Die Wahrscheinlichkeit für 3€ beträgt also 2/36=1/18.

Die Wahrscheinlichkeit für 50ct 18/36=½ und für -1€ 16/36=4/9.

E(X)=1/18 *3€ + ½*0,5€ - 4/9 € =-1/36 €

zu b)

E(X)=0€

Statt der 3€ muss der Auszahlungsbetrag a berechnet werden.

1/18 *a€ + ½*0,5€ - 4/9 €=0€ → a=3,5€

:-)

Comments

Hm, sicher?

>Ich nehme dabei an, dass es nur 0,5€ gibt, wenn beide Würfel die gleiche Gewinnzahl anzeigen.<

Versteh ich jetzt net -

> Ist unter den zwei Würfel(n) genau eine genannte Zahl<

Die gesamten Ereignisbilder müssten doch quasi mit 4 Würfel abgebildet werden können...

Ausschnitt aus 6^4

\(\begin{array}{|r|r|r|r|r|r|r|} w1&w2&r1&r2&3&1/2&0\\6&4&4&6&1&0&0&\\1 & 5 & 2 & 6 & 0 & 0 & 1 \\ 2 & 5 & 2 & 6 & 0 & 1 & 0 \\ 3 & 5 & 2 & 6 & 0 & 0 & 1 \\ 4 & 5 & 2 & 6 & 0 & 0 & 1 \\ 5 & 5 & 2 & 6 & 0 & 0 & 1 \\ 6 & 5 & 2 & 6 & 0 & 1 & 0 \\ 1 & 6 & 2 & 6 & 0 & 1 & 0 \\ 2 & 6 & 2 & 6 & 1 & 0 & 0 \\ 3 & 6 & 2 & 6 & 0 & 1 & 0 \\ 4 & 6 & 2 & 6 & 0 & 1 & 0 \\ 5 & 6 & 2 & 6 & 0 & 1 & 0 \\ 6 & 6 & 2 & 6 & 0 & 2 & 0 \\ \end{array}\)

wenn man diese Treffer auszählt erhalte ich

\(\begin{array}{rrr}66 & 600 & 630 \\5 & 0,5 & -1  \\330 & 300 & -630\end{array}\)

Kannst Du noch mal drüber schauen?

---

@wächter

Deine Tabelle verstehe ich so, dass w1 und w2 die gewählten und r1 und r2 die gewürfelten Zahlen sein sollen.

Da zwei verschiedene Zahlen gewählt werden, dürfen w1 und w2 nicht gleich sein.

Die letzte Zeile und entsprechend fünf weitere müssen daher gestrichen werden.

Außerdem multiplizierst du die 66 mit 5, obwohl nur 3€ vorgesehen sind.

Ich nehme dabei an, dass es nur 0,5€ gibt, wenn beide Würfel die gleiche Gewinnzahl anzeigen.

Damit meine ich:

Wenn z.B. die 1 und die 2 gewählt werden, die Würfel aber zwei Einsen (oder zwei Zweien) anzeigen, gibt es nur 50ct und keine 3€. Die 3€ gibt es nur bei 1 und 2 (bzw. 2 und 1).

---

Ne, anders rum w1,w2 gewürfelt r1,r2 geraten/gedacht

Auswertung in Spalte E,F,G

Zumindest geht die Auswertung auf

66 Dubletten, 600 Einzeltreffer, 630 Nieten bei 1296 Ereignisbilder

Klar, Doubletten ∩ Einzeltreffer = {}

meine Tabelle

https://docs.google.com/spreadsheets/d/11fU8ZUE_Vf0RcW79OraIOQoPR1zyLgGS/edit?usp=sharing&ouid=100849727549260862504&rtpof=true&sd=true

Die 5€ für eine Doublette würden ein faires Spiel ergeben...

---

Ich finde deine Vorgehensweise viel zu umständlich. Welche Zahlen vom Spieler gewählt werden, ist doch unwichtig. Daher muss ich doch keine 1296 Fälle durchspielen, von denen mindestens 6 gestrichen werden müssten.

Answer 2

a) \(2\cdot \left(\frac{1}{6}\right)^2\cdot 3€ + \left(2\cdot\frac{1}{6} \cdot\frac{5}{6}+ \frac{2}{3}\cdot\frac{1}{3}\right)\cdot 0{,}5€ + \left(\frac{2}{3}\right)^2\cdot (-1€)\)

b) Ersetze in dem korrekten Term aus a) die \(3€\) durch eine Variable, setze gleich Null und löse die Gleichung.

Die Lösung zu a) kommt aus folgendem Baumdiagramm

Answer 3

a) Berechnen Sie den erwarteten Gewinn des Spielers.

Sagen wir der Spieler wählt die Zahlen 3 und 4.

Die Wahrscheinlichkeit eine 3 zu würfeln beträgt 1/6 und die Wahrscheinlichkeit für eine 4 auch.

Also haben wir schon mal P(E) = 1/6 * 1/6.      P(E): Wahrscheinlichkeit, dass unser Erfolg eintritt.

Jetzt kann aber die 3 - 4 drei als erstes gewürfelt werden, aber genau so gut die 4 - 3 vier als erstes gewürfelt werden.

Somit müssen wir also noch das ganze mal zwei rechnen: P(E) = 1/6 * 1/6 * 2 = 2/32 = 1/16.

Nun können wir eine Tabelle für den Erwartungswert erstellen:

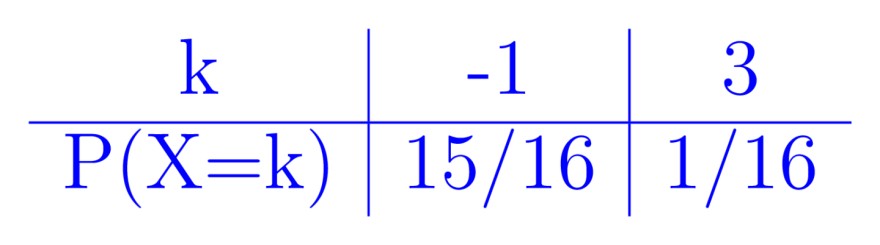
E(X) = 15/16 * (-1) + 1/16 * 3 = -0,75 [€]

A: Der erwartete Gewinn des Spieler beträgt also 75 Cent Verlust.

b) Wie viel müsste der Spieler im Fall erhalten, dass beide Würfel seine Zahlen zeigen,
damit es ein faires Spiel wäre?

Faires Spiel bedeutet weder Gewinn noch Verlust, also Erwartungswert = 0.

Um diese Aufgabe zu lösen, müssen wir eine Gleichung aufstellen.

E(X) = 15/16 * (-1) + 1/16 * x = 0

15/16 * (-1) + 1/16 * x = 0 | + 15/16
- 15/16  + 1/16 * x = 0 | + 15/16
 1/16 * x = 15/16     | : 1/16
  x = 15

Der Spieler muss also 15€ erhalten, damit es ein faires Spiel ist.

Comments

Das ist falsch.

---

Das ist falsch.

Yep.

Answer 4

Betrachten Sie folgendes Spiel: Ein Spieler wählt zwei verschiedene Zahlen
zwischen 1 und 6 und wirft 2 Würfel. Zeigen beide Würfel die genannten Zahlen an, erhält
er 3 Euro. Ist unter den zwei Würfel genau eine genannte Zahl, erhält er 0.5 Euro. Wenn
kein Würfel seine Zahlen anzeigt, muss der Spieler einen Euro zahlen.

a) Berechnen Sie den erwarteten Gewinn des Spielers.

Wahrscheinlichkeit bei genannter Zahlenwahl 1/36
Würfelwahrscheinlichkeit 1/36 für einen bestimmten
Wurf
Wahscheinlichkeit das das beide Zahlen übereinstimmen
1/36 * 1/36 = 1/1296

Dies Ereignis kann 36 mal vorkommen
 1 1 / 1  1
 1 2 / 1  2
usw bis
6 6 / 6 6

36 von 1296 = 2.78 %

Ich hatte in Wahrscheinlichkeitsrechnungen recht
häufig eigene Lösungsansätze.
Falls du übereinstimmts kann es weitergehen..

mfg Georg

Comments

Hallo Georg,

das ist leider falsch.

---

Hallo Monty,
zu a.)
ich habe mir deine Lösung noch nicht genau
angeschaut.
Werde ich aber noch.
Der mathecoach hat dasselbe wie ich
heraus.

An now something completely different

Denke daran
Dünn ist die Wand zwischen Wahnsinn und Verstand.
Du bist die Wand.

---

Der mathecoach hat dasselbe wie ich heraus.

Das stimmt nicht.

Du hast 2,78% raus, der Coach -2,78ct.

---

Ich schrieb
Wahrscheinlichkeit bei genannter Zahlenwahl 1/36
Würfelwahrscheinlichkeit 1/36 für einen bestimmten Wurf
Wahscheinlichkeit das das beide Zahlen übereinstimmen
1/36 * 1/36 = 1/1296

Dies Ereignis kann 36 mal vorkommen
1 1 / 1  1
1 2 / 1  2
usw bis
6 6 / 6 6

36 von 1296 = 2.78 %
Einer Wahrscheinlichkeit von minus
2.78 bin ich noch nicht begegnet..

Es läßt sich wahrscheinlich noch einfacher
argumentieren.

------------------------------

Gewinn 0.0278 * 3 € = 0.0834 €

Ist unter den zwei Würfeln genau eine genannte Zahl, erhält er 0.5 Euro.

Mögliche Zahlen unter den genannten
Zahlen : 1 bis 6, alle gleich wahrscheinlich.

Kombinationen
genannt / gewürfelt
1-1  2-1  3-1  ...
1-2  2-2  3-2
1-3  2-3  3-3
1-4  2-4  3-4
1-5  2-5  3-5
1-6  2-6  3-6

6 mal kann eine Zahl sowohl genannt als
auch gewürfelt vorkommen.
6 von 36 = 1/6 = 0.1666
Kommt die genannte Zahl bei 2.Wurf
auch vor spricht man von einem Pasch.
Beide Würfel zeigen daselbe.
Daselbe wie oben gewürfelt / gewürfelt
0.1666
Beide Ereignisse
( 6/36 ) * (6 / 36 ) = 2.78 %

Hierfür gibt es
0.5 € = 0.5 * 0.0278 = 0.0139 €

Gewinne
0.0278 * 3 € = 0.0834
0.0278 * 0.5 € = 0.0139 €
Summe Gegenwahrscheinlichkeiten
( 0.0278 + 0.0278 ) =  0.0556
Verlust
0.0556 * 1 = 0.0556
( 0.0834 + 0.0139 ) - 0.556
- 0.0417

Zitat
Karl May, Winnetou I, Sam Hawkins
" Wenn ich mich nicht irre " S.123
und andere Stellen

---

Hallo,

du musst berücksichtigen, dass zwei verschiedene Zahlen gewählt werden.

Answer 5

a) Berechnen Sie den erwarteten Gewinn des Spielers.

E = 3·2/6·1/6 + 0.5·(2·2/6·4/6 + 2/6·1/6) - 1·4/6·4/6 = - 1/36 = -0.02778 €

b) Wie viel müsste der Spieler im Fall erhalten, dass beide Würfel seine Zahlen zeigen, damit es ein faires Spiel wäre?

E = x·2/6·1/6 + 0.5·(2·2/6·4/6 + 2/6·1/6) - 1·4/6·4/6 = 0 → x = 3.50 €

Comments

Danke für die beste Erklärung! :)

---

Wäre es möglich dass sie erklären wie die Schritte bei + 0.5·(2·2/6·4/6 + 2/6·1/6) zustande kommen? Verstehe leider die Wahrscheinlichkeiten nicht. Danke und eine schöne Woche!