Bestimmen Sie c und n so, dass die Punkte P(-1|-0,5) und Q(2|4) auf dem Graphen der Funkton f(x)= c·x^n liegen.

Question

Aufgabe:

Bestimmen Sie c und n so, dass die Punkte P(-1|-0,5) und Q(2|4) auf dem Graphen der Funkton f(x)= c·x^n liegen.

Bitte mit Lösungsweg.

Answer 1

Hi,

Setze die beiden Punkte ein und erhalte so ein Gleichungssystem

-0,5 = c*(-1)^n

4 = c*2^n

 

Je nach c umformen und gleichsetzen:

-0,5/(-1)^n = 4/2^n   |*2^n *(-2)

(2/(-1))^n = -8

(-2)^n = -2^3

n = 3

 

Damit in die zweite Gleichung: c = 1/2

Folglich y = 1/2*x^3

 

Grüße

Comments

Danke dafür, kannst du mir noch genauer erklären wie man nach c umformt?

---

Du hast

4 = c*2^n   |:2^n

c = 4/2^n

im anderen Falle ist es genau das gleiche ;).

Klar?

Answer 2

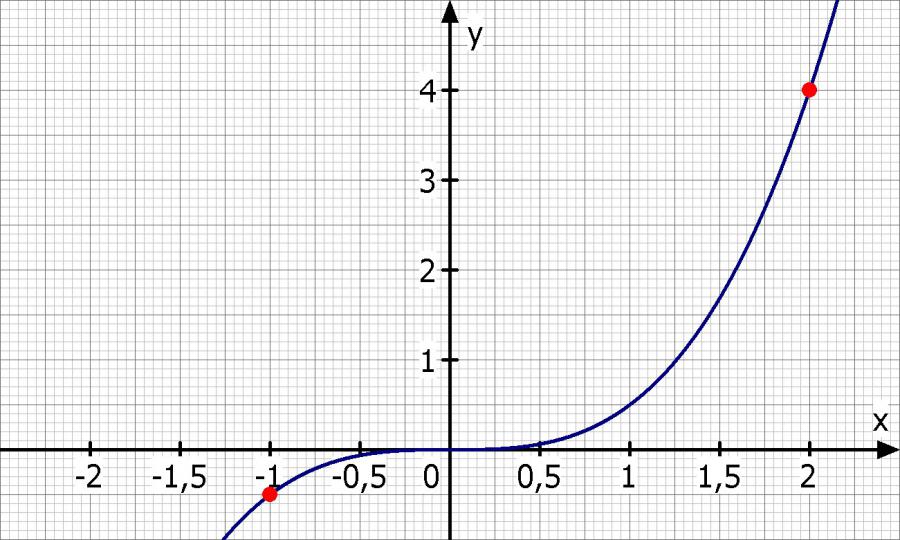
f(x) = c·x^n

f(-1) = -0.5
c·(-1)^n = -0.5

f(2) = 4
c·2^n = 4

Man darf hier z.B. auch das Divisionsverfahren anwenden. Man darf die beiden Gleichungen nicht nur Addieren sondern auch Dividieren.

c·(-1)^n / (c·2^n) = -0.5 / 4
(-1)^n / (2^n) = -1/8
(-1/2)^n = -1/8
n = 3

Nun das in eine Gleichung einsetzen und nach c auflösen

c·2^n = 4
c·2^3 = 4
c·8 = 4
c = 1/2

Damit lautet die Gleichung also 

f(x) = 1/2·x^3

Skizze: