Aufgabe:
Eine durch Bakterienpopulation vermehrt sich durch Zellteilung (alle Bakterien vermehren sich gleichzeitig). Die Bakterien kommen in zwei verschiedenen Genotypen vor. Zum einen der Wildtyp a, zum anderen die Mutante A. Der Zellzyklus besteht aus einer vegetativen und einer generativen Phase. In der vegetativen Phase stirbt ein Teil der Bakterien ab. Bei den a-Bakterien überlebt ein Anteil r (0 < r < 1). Bei den A-Bakterien überlebt nur ein Anteil (r/2). Bei der generativen Phase erfolgt die Zellteilung. Der Typ a geht durch Mutation mit der Wahrscheinlich m = 0,003 in den Typ A über, so dass aus einem a-Bakterium zwei A-Bakterien werden.
a.) Stellen Sie für beide Populationen (a, A) eine rekursive Vorschrift auf, welch die Bakterienmenge nach der generativen und vor der nächsten vegetativen Phase beschreibt.
(Tipp: für r= 0,6 gilt A_n+1 = 0,0036a_n + 0,6 A_n)
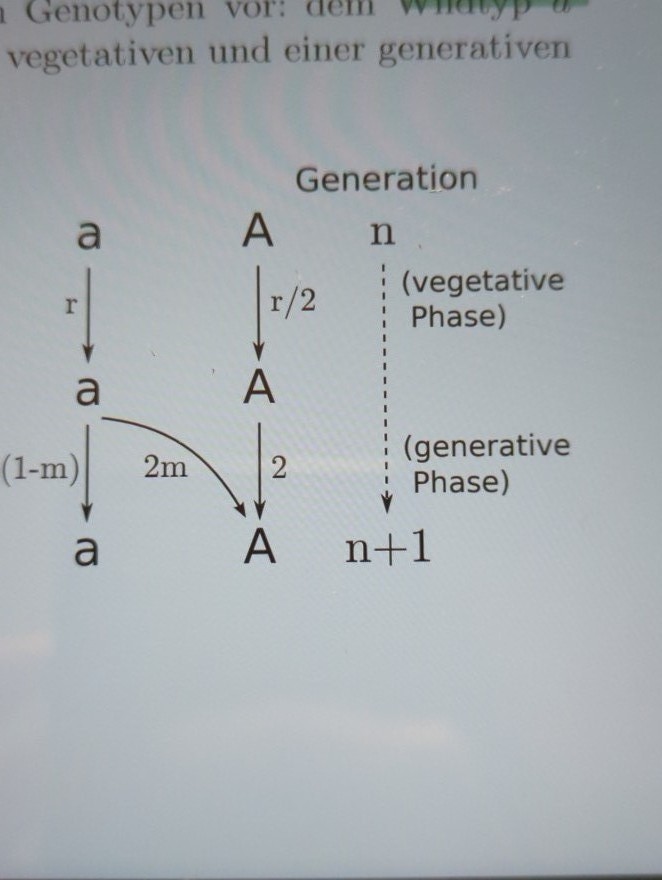
Problem/Ansatz:
Ich habe bereits versucht eine rekursive Folge zu entwickeln:
a_n+1 = (a_n * r) + 2 (1 -m)
Liebe Grüße
A.