Hallo,
berechne zunächst den Schnittpunkt S von f und g sowie den Schnittpunkt N von g mit der x-Achse.
[spoiler]
\(f(x)=x^2\quad g(x)=7x-6\\ x^2=7x-6\\ x^2-7x+6=0\\ x_1 =1\quad x_2=6\rightarrow S(1|1)\\[10pt] 7x-6=0\rightarrow N\big(\frac{6}{7}|0\big)\)
[/spoiler]
Berechne dann den Flächeninhalt zwischen f und der x-Achse von 0 bis 1 (blau) und ziehe davon die Fläche des schraffierten Dreiecks ab.
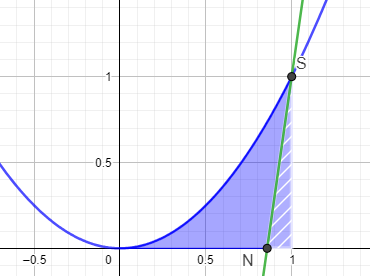
[spoiler]
\(\int \limits_{0}^{1}x^2\;dx=\bigg[\frac{1}{3}x^3\bigg]_0^1=\frac{1}{3}\\ A_\text{Dreieck}=\frac{1}{14}\\ \frac{1}{3}-\frac{1}{14}=\frac{11}{42}\approx 0,2619\)
[/spoiler]
Gruß, Silvia