Extremwertproblematik Flächeninhalt des Rechtecks maximal

Question

Aufgabe:

Gegeben ist die Funktion f mit f(x)= 1/6x^2 *(6-x).

Der Punkt P(ulv) mit 0<u<6 liegt auf dem Graphen von f. Die Koordinatenachsen und die Parallelen zu den Achsen durch P bilden ein Rechteck. Bestimmen Sie u so, dass der Flächeninhalt des Rechteckes maximal ist.Ist für diesen Wert von u der Umfang ebenfalls maximal?

Problem/Ansatz:

Ich weiß nicht was ich machen soll. Kann mir das bitte jemand ausführlich erklären wo setzt man an. Ich weiß dass ich hier Länge mal Breite machen muss und eine Nebenfunktion und Zielfunktion brauche..

Comments

Hallo

so Aufgaben fangen immer mit einem groben Plot von f(x) an. Ausnahmsweise hab ich den mal für dich gemacht, A=(u,f(u)) siehst du , B durch den Schnitt von y=f(u) mit f(x)  dann hast du alle Punkte in dem Rechteck.

Gruß lul

Answer 1

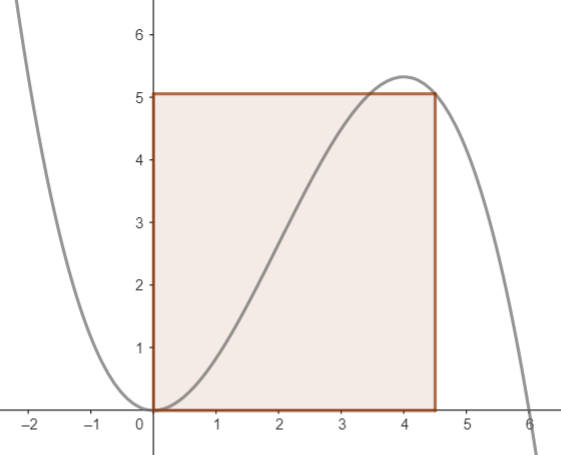
f(x) = 1/6·x^2·(6 - x) = x^2 - x^3/6

Die Fläche des entstehenden Rechtecks berechnet sich aus

A(u) = u·f(u) = u^3 - u^4/6

A'(u) = 3·u^2 - 2/3·u^3 = 0 --> u = 4.5

Jetzt schauen wir mal, ob das auch der Wert ist, für den der Umfang maximal wird.

U(u) = 2·u + 2·f(u) = - u^3/3 + 2·u^2 + 2·u

U'(u) = - u^2 + 4·u + 2 = 0 --> u = 2 + √6 = 4.449

Also nicht ganz.

Skizze