Aufgabe:
Hilfe gesucht
Problem/Ansatz:
Text erkannt:
Lacat/auth/RepositoryEntry/4495638563/CourseNode/106467521792831/test/0
4
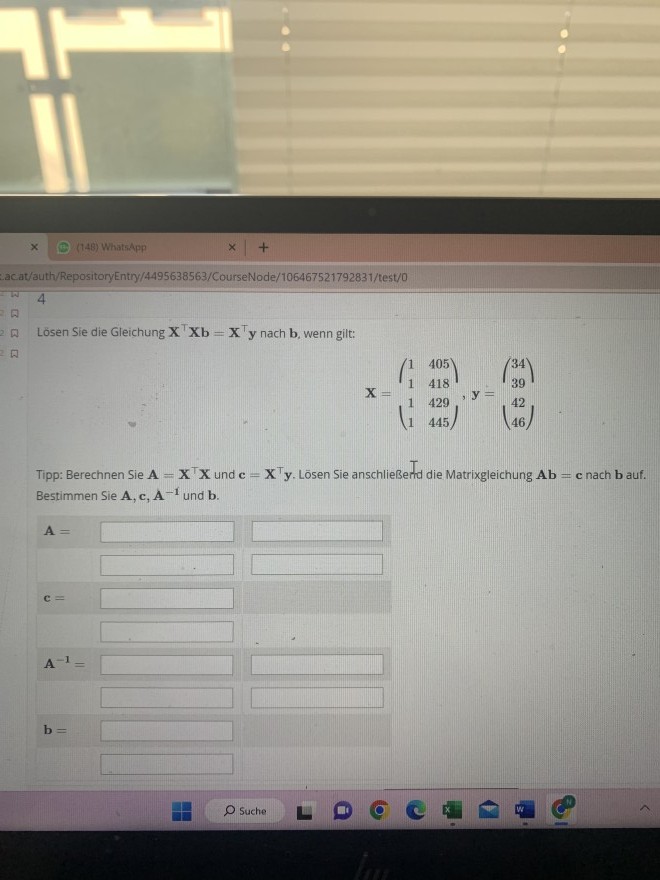
Losen Sie die Gleichung \( \mathbf{X}^{\top} \mathbf{X} \mathbf{b}=\mathbf{X}^{\top} \mathbf{y} \) nach \( \mathbf{b} \), wenn gilt:
\( \mathbf{X}=\frac{\left(\begin{array}{ll} 1 & 405 \\ 1 & 418 \end{array}\right)}{\left(\begin{array}{ll} 1 & 429 \\ 1 & 445 \end{array}\right)}, \mathbf{y}=\left(\begin{array}{l} 34 \\ 39 \end{array}\right) \)
Tipp: Berechnen Sie \( \mathbf{A}=\mathbf{X}^{\top} \mathbf{X} \) und \( \mathbf{c}=\mathbf{X}^{\top} \mathbf{y} \). Lösen Sie anschließernd die Matrixgleichung \( \mathbf{A} \mathbf{b}=\mathbf{c} \) nach \( \mathbf{b} \) auf. Bestimmen Sie \( \mathbf{A}, \mathbf{c}, \mathbf{A}^{-\mathbf{1}} \) und \( \mathbf{b} \).
\( \mathbf{A}= \)
\( \mathbf{c}= \)
\( \mathbf{A}^{-1}= \)
\( \mathbf{b}= \)
LG