Extremwertprobleme maximaler Flächeninhalt eines Dreiecks

Question

Aufgabe:

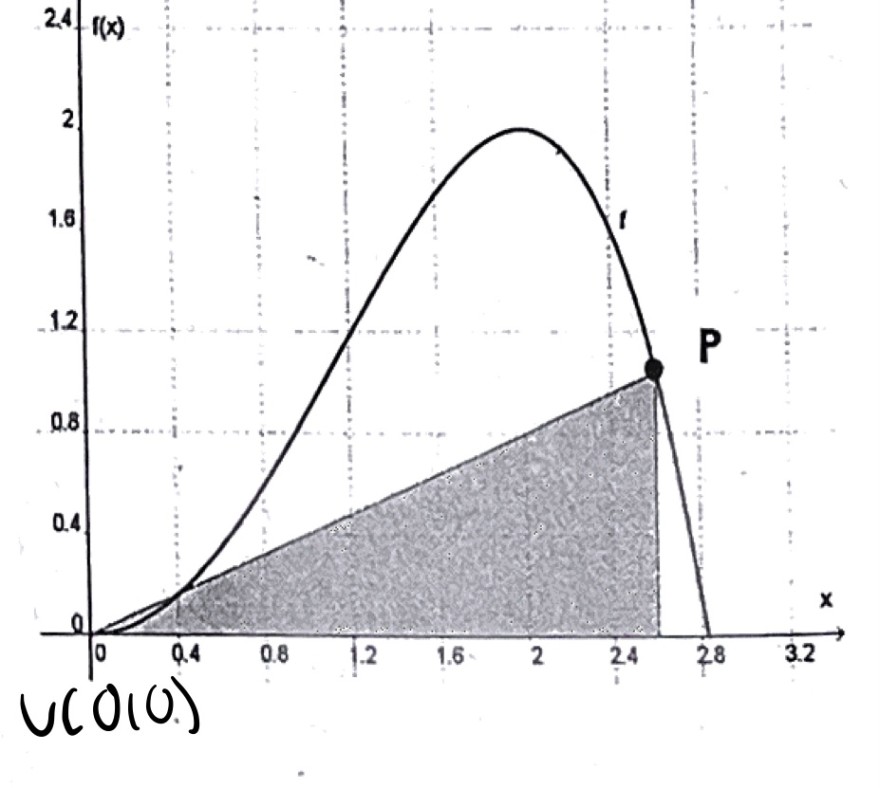
In Abb. Rechts ist der Graph der Funktion f mit f(x)=–1/8x⁴+x², 0<x<2.8 und ein beliebiges rechtwinkliges Dreieck gegeben. Der Flächeninhalt des rechtwinkligen Dreiecks soll im Intervall [0|2.8] maximal werden. Der linke untere Eckpunkt des Dreiecks liegt im Ursprung, der Rechte untere Eckpunkt auf der x–Achse zwischen 0 und 2.8. Die rechte obere Ecke liegt auf dem Punkt P. Am rechten unteren Eckpunkt liegt der rechte Winkel.

a) Ermitteln Sie wo P liegen muss, damit der Inhalt des Dreiecks maximal wird.

b) Bestimmen die den maximalen Flächeninhalt des Dreiecks.

[Zwischenergebnis: A(x)=–1/16x⁵+1/2x³]

Problem/Ansatz:

Hauptbedingung A= 1/2 x g x h

Nebenbedingung: –1/8u⁴+u²

In HB einsetzen:

A= 1/2 x u (–1/8u⁴+u²)

= –1/16u⁵+1/2u³

f‘(x)= –5/16x⁴+1.5x²

x1= -2.19 x2= 0 x3=0 x4= 2.19

f‘‘(x)= -5/4x³+3x

N.K:

f‘‘(x)= <0

f‘‘(2.19)= 8.4 cm³

f(2.19)= 1.92

Ist das alle so richtig gerechnet?

Welches Ergebnis ist jetzt aber für welche Aufgabe? Das verwirrt mich noch etwas…

Answer 1

Hallo

Deine Rechnung ist richtig für x=0 ist die Fläche ja 0 das Dreieck nur ein Punkt,  der negative Wert liegt ausserhalb des Definitionsgebietes.

a ) ist de Punkt (2,19,f(2,19 )

b) musst du noch die Fläche ausrechnen

(du solltest für Variable nicht 3 Namen benutzen  zuerst  g,h  dann u, dann x)

Gruß lul

Comments

Hallo Danke schonmal!

Meinst du für:

a) P(2.19|1.92) oder P(2.19|2.19)

b) wie errechnet man diesen?

danke

---

Hallo

mit der Formel dazu hast du doch angefangen? und natürlich liegt nur  P(2.19|1.92) auf der Kurve.

lul

Answer 2

"In Abb. Rechts ist der Graph der Funktion f mit $f(x)=–1/8x^4+x^2, 0<x<2.8$ und ein beliebiges rechtwinkliges Dreieck gegeben. Der Flächeninhalt des rechtwinkligen Dreiecks soll im Intervall [0|2.8] maximal werden. Der linke untere Eckpunkt des Dreiecks liegt im Ursprung, der Rechte untere Eckpunkt auf der x–Achse zwischen 0 und 2.8. Die rechte obere Ecke liegt auf dem Punkt P. Am rechten unteren Eckpunkt liegt der rechte Winkel."

$A(u)= \frac{1}{2}*u*(-\frac{1}{8}*u^4+u^2)=-\frac{1}{16}*u^5+\frac{1}{2}*u^3$ soll maximal werden.

$A´(u)=-\frac{5}{16}*u^4+\frac{3}{2}*u^2$

$-\frac{5}{16}*u^4+\frac{3}{2}*u^2=0$

$u^2*(-\frac{5}{16}u^2+\frac{3}{2})=0$

$u^2=0$ kommt nicht in Betracht.

$-\frac{5}{16}u^2+\frac{3}{2}=0$

$\frac{5}{16}u^2=\frac{3}{2}$

$u^2=\frac{3}{2}*\frac{16}{5}=4,8$

$u=\sqrt{4,8}$

Comments

Danke! Wie kommst du auf den Flächeninhalt?

---

ich mische mich einmal ein.

x-Stelle des Extremwerts
x = √ 4.8
y-Stelle
y = f ( x )

Die Fäche des Dreiecks ist

x * y / 2