\(fa(x)= x^2 * e^{-a*x}\) mit \(a=0,2\)
\(f(x)= x^2 * e^{-0,2*x}\)
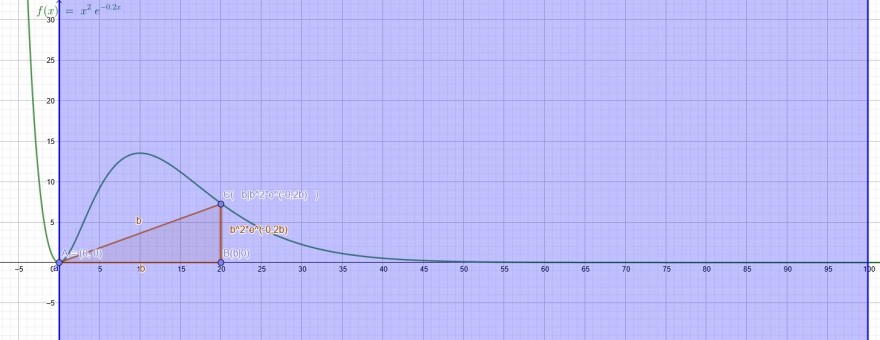
Siehe unten die Zeichnung
\(A(b)= \frac{b*(b^2*e^{-0,2b})}{2} \) soll maximal werden.
\(A(b)= \frac{b^3*e^{-0,2b}}{2} \)
\(A´(b)= \frac{3b^2*e^{-0,2b}+b^3*e^{-0,2b}*(-0,2)}{2} \)
\(A´(b)= \frac{3b^2*e^{-0,2b}-0,2*b^3*e^{-0,2b}}{2} \)
\(\frac{3b^2*e^{-0,2b}-0,2*b^3*e^{-0,2b}}{2}=0 \)
\(3b^2*e^{-0,2b}-0,2*b^3*e^{-0,2b}=0 \)
\(e^{-0,2b}*( 3b^2-0,2*b^3)=0 \)
\(e^{-0,2b}≠0 \)
\(3b^2-0,2*b^3=0 \)
\(b^2*(3-0,2*b)=0 \)
\(b=0 \) kommt nicht in Betracht
\(3-0,2*b=0 \) \(b=15 \)
Beachte bitte bei der Hypotenuse das b nicht.