Aufgabe: Bestimme α ∈ ℝ so, dass die folgende Funktion stetig wird:
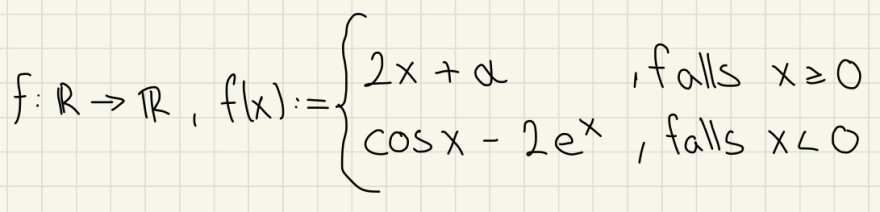
Text erkannt:
\( f: \mathbb{R} \rightarrow \mathbb{R}, f(x):=\left\{\begin{array}{ll}2 x+\alpha, & \text { falls } x \geq 0 \\ \cos x-2 e^{x}, & \text { falls } x<0\end{array}\right. \)
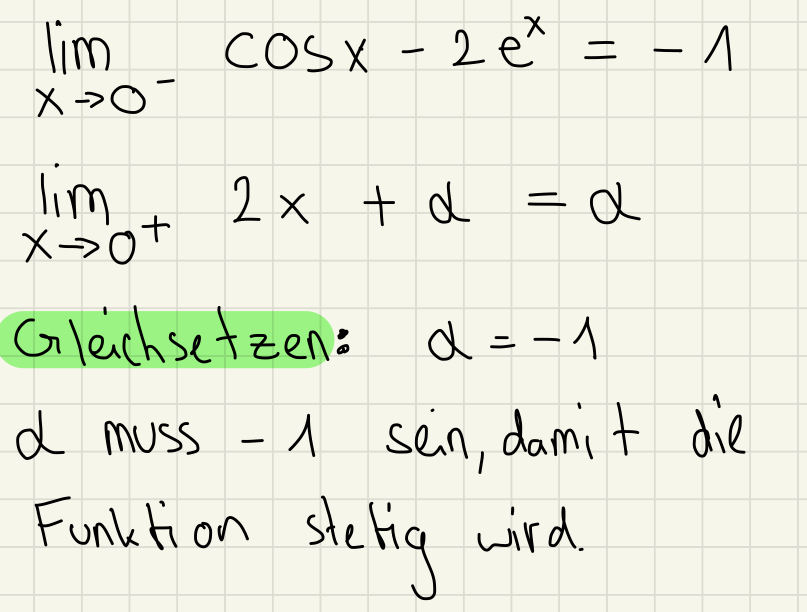
Text erkannt:
\( \begin{array}{l} \lim \limits_{x \rightarrow 0^{-}} \cos x-2 e^{x}=-1 \\ \lim \limits_{x \rightarrow 0^{+}} 2 x+\alpha=\alpha \end{array} \)
Glachsetzen: \( \alpha=-1 \)
d muss - 1 sein, damit die
Funktion stetig wird.
Problem/Ansatz:
Weiß nicht ob es richtig ist