Untersuche beide Reihen auf Konvergenz

Question

Aufgabe:

Untersuche die Reihen auf Konvergenz:

a) \( \sum \limits_{n=1}^{\infty} \frac{8^{n}}{\sqrt{n !}} \)

b) \( \sum \limits_{n=1}^{\infty} \frac{1}{n^{2}}\left(\begin{array}{l}n \\ 2\end{array}\right) \)

Answer 1

Hallo,

bei der a) kann man das Wurzelkriterium anwenden. Sei \(a_n=\frac{8^n}{\sqrt{n!}}\). Ich setze voraus, dass du weißt, dass \(\sqrt[n]{n!}\to \infty\), wenn \(n\to \infty\). Wenn nicht: Zeige per Induktion die Abschätzung \(n!\geq \left(\frac{n}{2}\right)^{n/2}\). Es gilt:$$\sqrt[n]{\left|\frac{8^n}{\sqrt{n!}}\right|}=\frac{8}{\sqrt[n+1]{n!}}\xrightarrow{n\to \infty}0,$$ daher konvergiert die Reihe absolut nach dem Wurzelkriterium. Ich habe WolframAlpha das mal approximieren lassen für eine Millionen Summanden (das stagniert)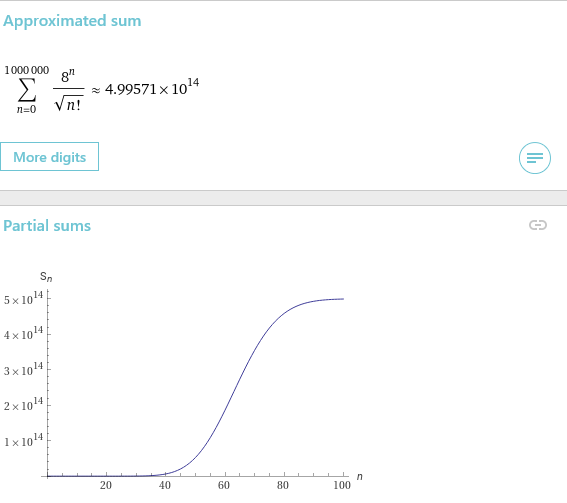

Das ist sicher irgendeine algebraisch manipulierte Einsetzungsinstanz der e-Reihe.

(b) Das ist divergent nach dem Trivialkriterium. Rechne den Binomialkoeffizienten aus und zeigen, dass die entsehende Folge nicht gegen 0 konvergiert.