Hallo :)
Ich weiß leider einfach nicht, wie ich diese Hausaufgabe lösen soll. Vielleicht kann mir jemand helfen. Die Aufgabe lautet:
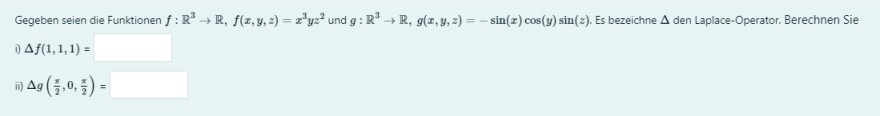
Text erkannt:
Gegeben seien die Funktionen \( f: \mathbb{R}^{3} \rightarrow \mathbb{R}, f(x, y, z)=x^{3} y z^{2} \) und \( g: \mathbb{R}^{3} \rightarrow \mathbb{R}, g(x, y, z)=-\sin (x) \cos (y) \sin (z) \). Es bezeichne \( \Delta \) den Laplace-Operator. Berechnen Sie
i) \( \Delta f(1,1,1)= \)
ii) \( \Delta g\left(\frac{\pi}{2}, 0, \frac{\pi}{2}\right)= \)
Vielen Dank an alle die mir helfen können!