Bestimmen Sie die Ableitungsfunktion F‘ von der Funktion F (Differenzialquotient)

Question

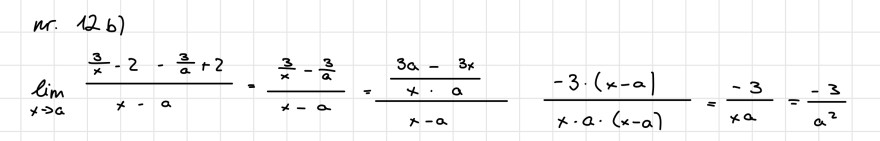
Text erkannt:

n. \( 12 b \) )
\( \lim \limits_{x \rightarrow a} \frac{\frac{3}{x}-2-\frac{3}{a}+2}{x-a}=\frac{\frac{3}{x}-\frac{3}{a}}{x-a}=\frac{\frac{3 a-3 x}{x \cdot a}}{x-a} \quad \frac{-3 \cdot(x-a)}{x \cdot a \cdot(x-a)}=\frac{-3}{x a}=\frac{-3}{a^{2}} \)

Aufgabe:

Bestimmen Sie die Ableitungsfunktion F‘ von der Funktion F

f(x)= 3/x -2

Ich verstehe allerdings den Übergang von Schritt 2 auf Schritt 3 nicht ( multipliziert man dort mit etwas?)

Problem/Ansatz:

Man darf ausschließen mit dem Differenzialquotienten arbeiten, nicht mit dem normalen Ableiten von wegen Hochzahl nach vorne multiplizieren und Hochzahl Minus 1

Answer 1

Hallo,

der Hauptnenner der beiden Brüche ist ax bzw. xa. Auf den wurden sie jeweils durch Erweiterung gebracht:

\(\frac{3}{x}=\frac{3\cdot a}{x\cdot a}=\frac{3a}{x\cdot a}\\ \frac{3}{a}=\frac{3\cdot x}{a\cdot x}=\frac{3x}{x\cdot a}\)

Damit ist der Zähler \(\frac{3}{x}-\frac{3}{a}=\frac{3a-3x}{x\cdot a}\)

Gruß, Silvia

Comments

Außerdem wird die funktion für f(x) in der Formel vom differenzenquotienten eingesetzt (substituiert), also muss diese in Klammern gesetzt werden (wie auch zum Beispiel bei Gleichungssystemen).