Die gleiche Frage ist hier zwar schon drinnen, aber sie hilft keinem weiter. Lösung + Weg wäre nett.
Deshalb stelle ich sie nochmal rein.
Ja, beides stimmt.
Hier noch mal die Eingabemaske:
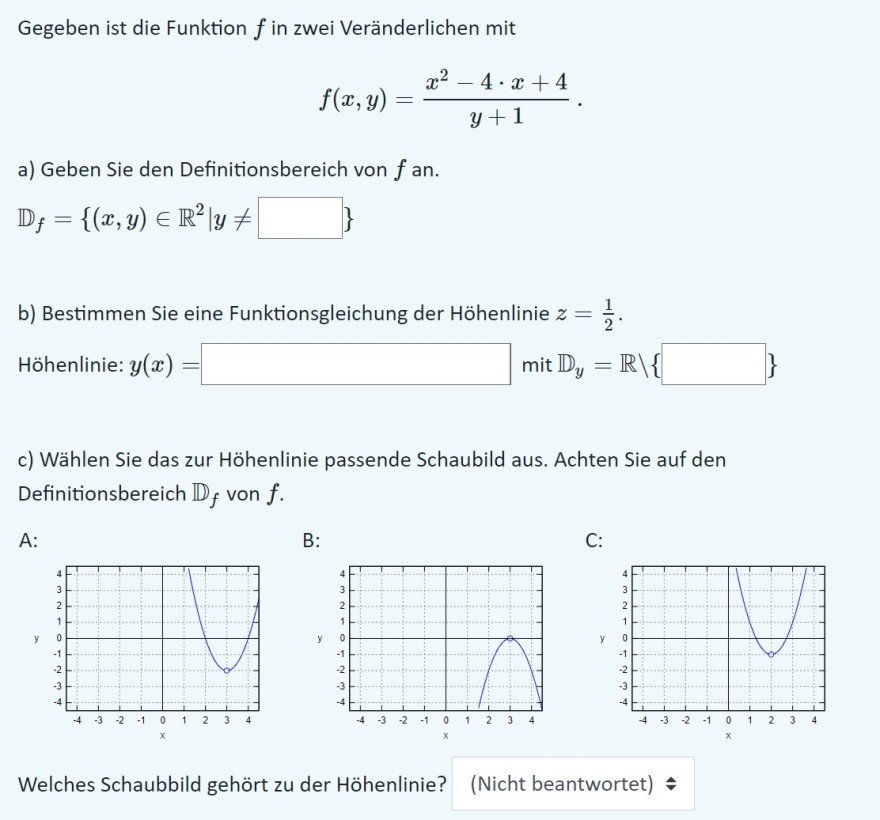
Gegeben ist die Funktion \( f \) in zwei Veränderlichen mit
$$ f(x, y)=\frac{x^{2}-4 \cdot x+4}{y+1}. $$
a) Geben Sie den Definitionsbereich von \( f \) an.
$$ \mathbb{D}_{f}=\left\{(x, y) \in \mathbb{R}^{2} \mid y \neq\green{-1} \right\}.$$
b) Bestimmen Sie eine Funktionsgleichung der Höhenlinie \( z=\frac{1}{2}.\)
Höhenlinie: \( \quad\green{y(x)=2\cdot\left(x-2\right)^2-1}\quad \) mit \( \quad\mathbb{D}_{y}=\mathbb{R} \backslash\left\{\green{2}\right\}\)
c) Wählen Sie das zur Höhenlinie passende Schaubild aus.
Achten Sie auf den Definitionsbereich \( \mathbb{D}_{f} \) von \( f \).
Welches Schaubbild gehört zu der Höhenlinie?
Wähle A, B oder C.