Numerische Verfahren: Fehlerabschätzung

Question

Aufgabe: Zeigen Sie, dass für u ∈ C∞(R) gilt:

Text erkannt:

\( \frac{u(\bar{x}-h)-2 u(\bar{x})+u(\bar{x}+h)}{h^{2}}-u^{\prime \prime}(\bar{x})=\mathcal{O}\left(h^{2}\right) \)

Hinweis: Betrachten Sie die Taylorentwicklung von u(x̄-h) und u(x̄-h) um den Punkt x̄

Problem: Ich verstehe hier leider nicht wie man das macht :)

Answer 1

Laut Taylor gilt

\(u(\bar x + h) = u(\bar x) + u'(\bar x)h + \frac{u''(\bar x)}{2}h^2  + \frac{u^{(3)}(\bar x)}{6}h^3 +O(h^4) \)

\(u(\bar x - h) = u(\bar x) - u'(\bar x)h + \frac{u''(\bar x)}{2}h^2  - \frac{u^{(3)}(\bar x)}{6}h^3 + O(h^4)  \).

Jetzt addierst du die beiden Gleichungen und stellst um und beachtest, dass \(O(h^4)+O(h^4) = O(h^4)\) und \(\frac{O(h^4)}{h^2}= O(h^2)\) ist:

\(u(\bar x + h) - 2 u(\bar x) + u(\bar x - h) =  u''(\bar x)h^2  + O(h^4)  \)

\(\Rightarrow \frac{u(\bar x + h) - 2 u(\bar x) + u(\bar x - h)}{h^2} - u''(\bar x) = O(h^2)\)

Comments

Ah verstehe

Danke vielmals :)

---

Auch wenn es die beste Antwort ist, trancelocation hat vergessen, O(h^2) durch h^2 zu dividieren.

---

@mathhilf
Stimmt. Pass ich entsprechend an. Danke für den Hinweis.

Answer 2

Aloha :)

Willkommen in der Mathelounge... \o/

Wir folgen dem Rezept des Kochs und betrachten die besagten Taylor-Entwicklungen:$$u(x\pm h)=u(x)\pm u'(x)\,h+\frac{u''(x)}{2}\,h^2\pm\frac{u'''(x)}{6}\,h^3+\frac{u''''(x)}{24}\,h^4+O(h^5)$$Diese setzen wir in die Formel aus der Aufgabenstellung ein:$$\phantom=\frac{u(x+h)+u(x-h)-2u(x)}{h^2}-u''(x)$$$$=\frac{2\,\frac{u''(x)}{2}\,h^2+2\,\frac{u''''(x)}{24}\,h^4+O(h^6)}{h^2}-u''(x)$$$$=\frac{u''''(x)}{12}h^2=O(h^2)$$

Comments

Danke,

ich verstehe wie sich die Taylorentwicklung als unendliche Reihe zusammensetzt, jedoch kann ich nicht ganz nachvollziehen wie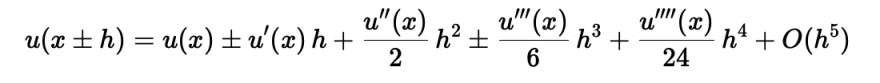

Text erkannt:

\( u(x \pm h)=u(x) \pm u^{\prime}(x) h+\frac{u^{\prime \prime}(x)}{2} h^{2} \pm \frac{u^{\prime \prime \prime}(x)}{6} h^{3}+\frac{u^{\prime \prime \prime \prime}(x)}{24} h^{4}+O\left(h^{5}\right) \)

denn in meinem Skript steht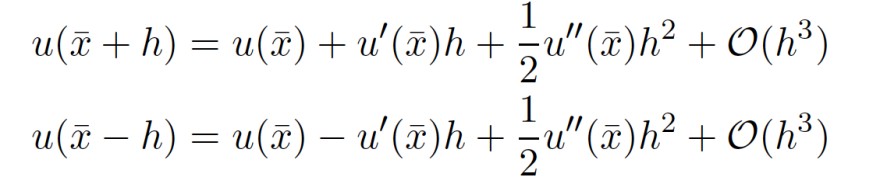

Text erkannt:

\( u(\bar{x}+h)=u(\bar{x})+u^{\prime}(\bar{x}) h+\frac{1}{2} u^{\prime \prime}(\bar{x}) h^{2}+\mathcal{O}\left(h^{3}\right) \)
\( u(\bar{x}-h)=u(\bar{x})-u^{\prime}(\bar{x}) h+\frac{1}{2} u^{\prime \prime}(\bar{x}) h^{2}+\mathcal{O}\left(h^{3}\right) \)

Könnten Sie das vielleicht nochmal erläutern?

---

Sorry ich habe das Falsche reingestellt. Die Taylorreihe ich mir verständlich geworden. Aber könnten Sie vielleicht die Anzahl der Zwischenschritte erhöhen, da mir z.B der Sprung von der Aufgabenstellungsgleichung zur nächsten Gleichung (hier: die nach dem ersten =) nicht ganz klar geworden ist :)