Aufgabe:
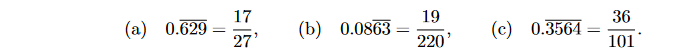
Text erkannt:
(a) \( 0 . \overline{629}=\frac{17}{27} \),
(b) \( 0.08 \overline{63}=\frac{19}{220} \),
(c) \( 0 . \overline{3564}=\frac{36}{101} \).
Es soll mit Hilfe dieses Beispiels:
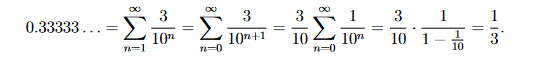
Text erkannt:
\( 0.33333 \ldots=\sum \limits_{n=1}^{\infty} \frac{3}{10^{n}}=\sum \limits_{n=0}^{\infty} \frac{3}{10^{n+1}}=\frac{3}{10} \sum \limits_{n=0}^{\infty} \frac{1}{10^{n}}=\frac{3}{10} \cdot \frac{1}{1-\frac{1}{10}}=\frac{1}{3} \).
gezeigt werden, dass die Aussagen gelten.
Problem/Ansatz:
Ich habe viel herumprobiert und finde jedoch keinen Ansatz.
Ich bedanke mich schon einmal im Voraus für jede Hilfe.