Hallo,
Du bekommst schließlich 6 Gleichungen mit 6 Variablen.(2 Gleichungen fallen weg, sind redundant)
Damit mußt Du freie Koeffizienten wählen und die restlichen Gleichungen durch Sie ausdrücken.
Ich habe erhalten:

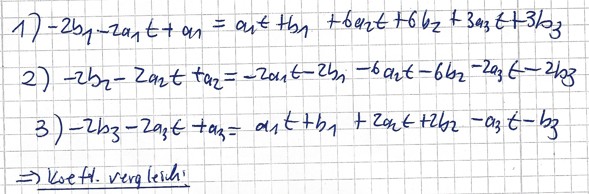
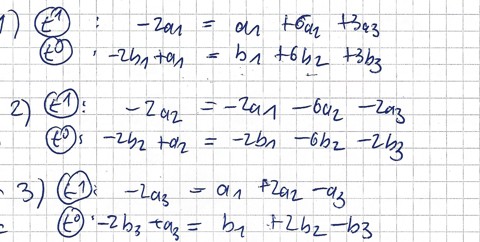
A) 0 = 3a1 +6a2 +3a3
B) 0= 3b1+6b2+ 3b3 -a1
C) 0= -2a1 -4a2-2a3 ->redundant
D) 0=-2b1-4b2-2b2-a2
E) 0= a1 +2a2+a3 -->redundant
F) 0= b1+2b2 +b3-a3
usw.
Ich verwende in solchen Fällen lieber die Hauptvektormethode (falls behandelt)
Sicher sind das dann möglicherweise andere Bezeichnungen als ich habe.

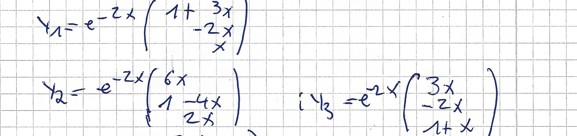
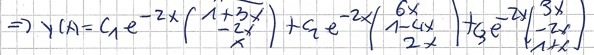
Kontrolle Wolfram Alpha:
\( \mathrm{y} 1(x)=c_{1} e^{-2 x}(3 x+1)+6 c_{2} e^{-2 x} x+3 c_{3} e^{-2 x} x \)
\( \mathrm{y} 2(x)=-2 c_{1} e^{-2 x} x-c_{2} e^{-2 x}(4 x-1)-2 c_{3} e^{-2 x} x \)
\( \mathrm{y} 3(x)=c_{1} e^{-2 x} x+2 c_{2} e^{-2 x} x+c_{3} e^{-2 x}(x+1) \)