Aufgabe:

Text erkannt:
Lösen Sie die folgenden Integrale, in dem Sie im ersten Integrationsschritt die Methode der partiellen Integration anwenden:
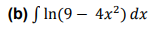
Text erkannt:
(b) \( \int \ln \left(9-4 x^{2}\right) d x \)
Problem/Ansatz:
Partielle Integration:
f(x) = ln(9-4x^2)
f'(x) = \( \frac{-8x}{9-4x^{2}} \)
g'(x) = 1
g(x) = x
Daher: x*ln(9-4x^2) + 8\( \int\limits_{}^{} \) \( \frac{x^{2}}{9-4x^{2}} \)
Ab hier weiß ich nicht weiter. Wie integriere ich das weiter? Ich habe schon mit der Substitutionsmethode weiter integriert, aber da kommt nicht das richtige raus.
Vielen Dank für die Hilfe! :)