Aufgabe:
Hallo ich habe die Singulärwertzerlegung der folgenden Matrix A geprüft, jedoch geht da was nicht ganz auf.
Text erkannt:
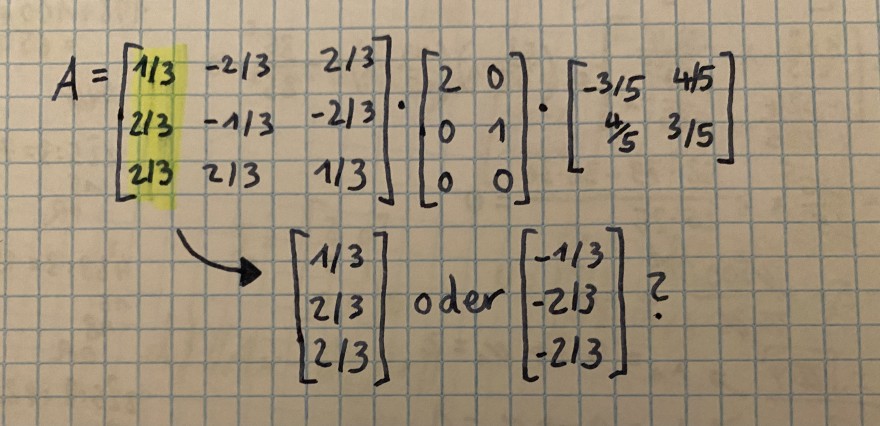
\( A=\left[\begin{array}{ccc}1 / 3 & -2 / 3 & 2 / 3 \\ 2 / 3 & -1 / 3 & -2 / 3 \\ 2 / 3 & 2 / 3 & 1 / 3\end{array}\right] \cdot\left[\begin{array}{ll}2 & 0 \\ 0 & 1 \\ 0 & 0\end{array}\right] \cdot\left[\begin{array}{cc}-3 / 5 & 4 / 5 \\ 4 / 5 & 3 / 5\end{array}\right] \)
\( \rightarrow\left[\begin{array}{l}1 / 3 \\ 2 / 3 \\ 2 / 3\end{array}\right] \) oder \( \left[\begin{array}{l}-1 / 3 \\ -2 / 3 \\ -2 / 3\end{array}\right] ? \)
Problem/Ansatz:
Eigentlich sollte ich ja dadurch wieder die Matrix A erhalten, allerdings habe ich das nachgeprüft und es kommt was anderes raus. Selbst Singulärwertzerlegungsrechner auf Websiten geben mir die gleichen U und V Matrizen.
Komisch ist wenn ich den ersten Spaltenvektor der U Matrix (gelb markiert) mit *(-1) multipliziere, dass auf einmal das richtige rauskommt. (Zur Info: Zuvor waren alle seine Einträge negativ, jedoch dachte ich es macht keinen Unterschied wenn ich sie alle mit *(-1) multipliziere).
Allerdings dachte ich immer, dass es völlig egal ist ob ich einen Spaltenvektor so oder denselben Vektor *(-1) davon nehme.
Spielt das eine Rolle und muss ich dann den dazugehörigen Singulärwert ebenfalls mal *(-1) rechnen?