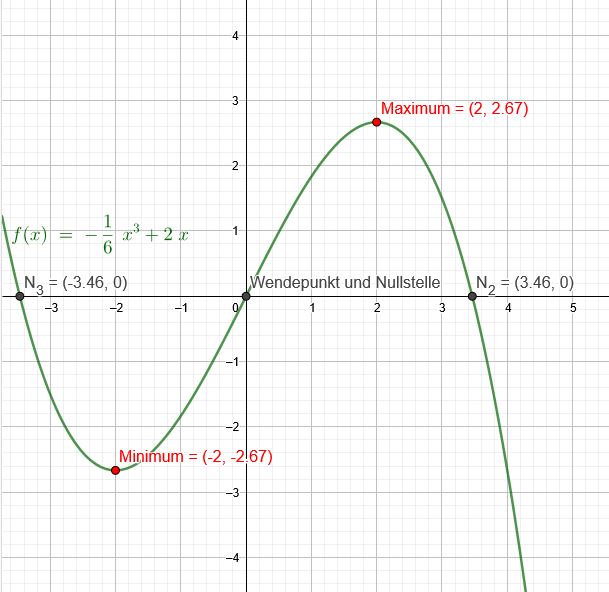
\(f(x) =- \frac{1}{6} *x^3+2x\)
Nullstellen:
\(- \frac{1}{6} *x^3+2x=0|*6\)
\(- x^3+12x=0 |*(-1)\)
\( x^3-12x=0\)
Nun x ausklammern:
\( x*(x^2-12)=0\)
\( x₁=0\)
\( x^2-12=0 |+12\)
\( x^2=12 |\sqrt{~~}\)
\( x₂=\sqrt{12}=\sqrt{4*3}=2*\sqrt{3}\)
\( x₃=-\sqrt{12}=-\sqrt{4*3}=-2*\sqrt{3}\)
Schnitt mit der y-Achse:
\(f(0) =- \frac{1}{6} *0^3+2*0=0\)
Extremwerte:
\(f´(x) =- \frac{3}{6} *x^2+2=- \frac{1}{2} *x^2+2\)
\(- \frac{1}{2} *x^2+2=0\)
\(x^2=4\)
\(x₁=2\) \(f(2) =- \frac{1}{6} *2^3+2*2=- \frac{1}{6} *8+4=\frac{8}{3}\)
\(x₂=-2\) \(f(-2) =- \frac{1}{6} *(-2) ^3+2*(-2) =- \frac{1}{6} *(-8)-4=-\frac{8}{3}\)
Art des Extremwertes:
\(f´´(x) =- \frac{2}{2} *x=-x\)
\(f´´(2) =-2<0\) Maximum
\(f´´(-2) =2>0\) Minimum
Wendepunkt:
\(f´´(x) =-x\)
\(x=0\) \(f(0)=0\)