Ich habe eine Frage zu Grenzwerten und der Eulerzahl.
Wir hatten in der Vorlesung die Grenzwerte einer bestimmten "Art" von Funktion durch die Definition der Eulerzahl festgelegt:
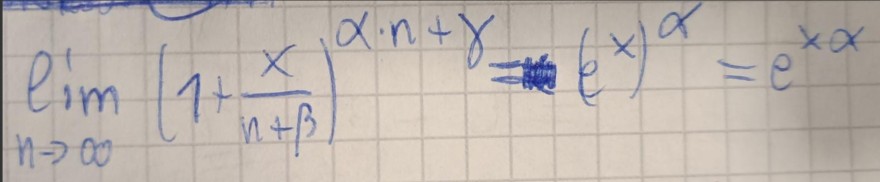
Text erkannt:
\( \lim \limits_{n \rightarrow \infty}\left(1+\frac{x}{n+\beta}\right)^{\alpha \cdot n+\gamma}=\left(e^{x}\right)^{\alpha}=e^{x \alpha} \)
Jetzt hatte ich folgende Aufgabe:
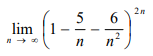
Text erkannt:
\( \lim \limits_{n \rightarrow \infty}\left(1-\frac{5}{n}-\frac{6}{n^{2}}\right)^{2 n} \)
Man kann die natürlich durch umstellen etc. lösen und kommt dann auf e^-10.
Ich hatte so argumentiert, dass 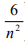 aufgrund der Potenz unter dem Bruch als null zu werten ist, weil es deutlich schneller gegen 0 geht. Dann bleibt nur noch der übliche Teil und man hat e^(-5*2), also e^-10.
aufgrund der Potenz unter dem Bruch als null zu werten ist, weil es deutlich schneller gegen 0 geht. Dann bleibt nur noch der übliche Teil und man hat e^(-5*2), also e^-10.
Ich habe das jetzt schon bei ein paar dieser Funktionen gemacht und es kam immer das richtige Ergebnis raus.
Zum Beispiel:
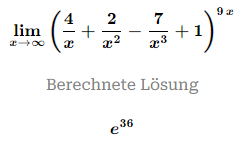
Text erkannt:
\( \lim \limits_{x \rightarrow \infty}\left(\frac{4}{x}+\frac{2}{x^{2}}-\frac{7}{x^{3}}+1\right)^{9 x} \)
Berechnete Lösung
\( e^{36} \)
Mein Weg: Die beiden mit x^2 und x^3 "ignorieren" und dann e^(4*9)
Text erkannt:
\( \lim \limits_{x \rightarrow \infty}\left(-\frac{2}{x}+\frac{2}{x^{2}}-\frac{6}{x^{5}}+1\right)^{5 x} \)
Berechnete Lösung
\( \frac{1}{e^{10}} \)
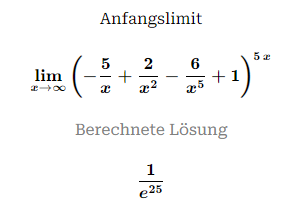
Text erkannt:
\( \lim \limits_{x \rightarrow \infty}\left(-\frac{2}{x}+\frac{2}{x^{2}}-\frac{6}{x^{5}}+1\right)^{5 x} \)
Berechnete Lösung
\( \frac{1}{e^{10}} \)
Hier ebenfalls direkt e^(-5*5)
Ich hoffe man versteht, was ich meine ^^
Mir fehlt in unserer Definition die Beachtung weiterer Brüche in der Funktion. Oder wurden diese extra nicht beachtet, weil sie irrelevant sind? In der Vorlesung wurde nichts dazu gesagt.
Ist das Zufall? Gibt's dazu eine Erweiterung der Regel, die wir nicht hatten? Kann mir jemand ein Beispiel zeigen, bei dem das nicht geht, falls es Zufall war, bzw. man es so nicht immer machen kann?
Vielen Dank schonmal für die Mühe ^^