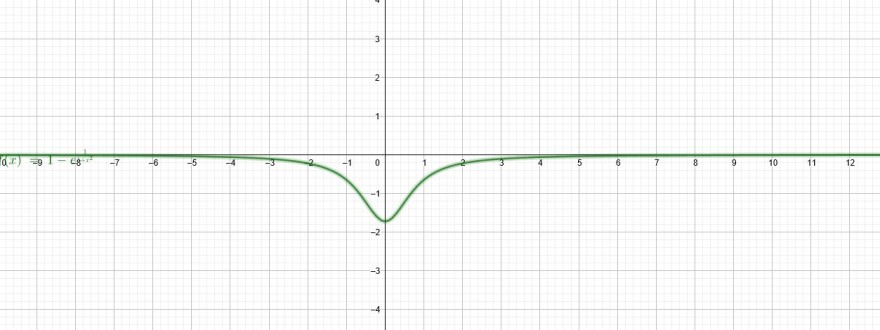
Zeigen Sie, dass die Funktion g(x) = 1 − e^(1/1+x^2) ein Minimum über den reellen Zahlen besitzt.

Question

Aufgabe:

Zeigen Sie, dass die Funktion g(x) = 1 − e^(1/1+x^2) ein Minimum über den reellen Zahlen besitzt.

Problem/Ansatz:

Wie kann ich das zeigen ? Muss ich es mit limes zeigen ?

Vielen Dank !

Comments

Zeigen Sie, wo die Klammern fehlen in der abgetippten Aufgabe.

---

Die Funktion lautet g(x)=1 − e^(1/(1+x2)). Ist es das was sie meinen ?

---

g ist die Verkettung   g =  f1 o f2 o f3 o f4 o f1 o f5  mit
f1(x) = 1+x , f2(x) = -x , f3(x) = e^x , f4(x) = 1/x , f5(x) = x^2
überlege dir, welche Funktionen welche Art von Extremum haben und welche Funktionen welche Art von Monotonie aufweisen.

---

@mathefreund ich weiss es nicht, das kannst nur Du wissen was in der Aufgabe steht. Vielleicht bin ich ja schrecklich vorgestern, aber ich vertrete die Ansicht, man soll sagen was die Frage ist, wenn man eine Frage hat und Antworten sucht.

Answer 1

Aloha :)

Kandidaten für Extremstellen der Funktion$$g(x)=1-e^{\frac{1}{1+x^2}}$$finden wir dort, wo die erste Ableitung verschwindet. Die \(1\) in dem Term ist eine Konstante und interessiert uns beim Ableiten nicht. Die Exponentialfunktion knacken wir mit zweifacher Anwendung der Kettenregel:$$0\stackrel!=g'(x)=\left(-e^{\pink{\frac{1}{1+x^2}}}\right)'=\underbrace{-e^{\pink{\frac{1}{1+x^2}}}}_{\text{äußere Abl.}}\cdot\underbrace{\left(\pink{\frac{1}{1+x^2}}\right)'}_{=\text{innere Abl.}}=-e^{\frac{1}{1+x^2}}\left((1+\green{x^2})^{-1}\right)'$$$$\phantom 0=-e^{\frac{1}{1+x^2}}\underbrace{\left(-(1+\green{x^2})^{-2}\right)}_{\text{äußere Abl.}}\cdot\underbrace{\left(\green{2x}\right)}_{=\text{innere Abl.}}=e^{\frac{1}{1+x^2}}\cdot\frac{2x}{(1+x^2)^2}$$Da die Exponentialfunktion stets positiv ist, kann nur der Bruch zu \(0\) werden, was nur für \(x=0\) der Fall ist. Da überdies auch der Nenner des Bruches stets positiv ist, wechselt die erste Ableitung bei \(x=0\) ihr Vorzeichen von negativ für \(x<0\) zu positiv für \(x>0\). Das heißt \(f(x)\) fällt für \(x<0\) und steigt für \(x>0\).

Daher hat die Funktion an der Stelle \(x=0\) ein globales Minimum.

Answer 2

f '(x) = 0

Ergebnis in f ''(x)

Mininum, falls f''(x) >0

https://www.ableitungsrechner.net/

Answer 3

Ohne Ableitung ?

Es ist wohl g(x) = 1 − e^(1/(1+x²)).

Zeige: Es ist eine überall definierte stetige Funktion

deren Graph symmetrisch zur y-Achse verläuft

und es ist  f(0)<0  und die Grenzwerte für x gegen ±∞

sind beide 0.

Comments

Wir dürfen nicht ableiten. Soll ich die Stetigkeit mit Limes zeigen, indem ich es einmal gegen plus und dann gegen minus unendlich laufen lasse ?

---

Stetigkeit folgt doch aus der Zusammensetzung durch

stetige Funktionen.

Answer 4

Zeigen Sie, dass die Funktion  \(g(x) = 1 − e^{\frac{1}{1+x^2}}\)ein Minimum über den reellen Zahlen besitzt

\(g(x) = 1 − e^{\frac{1}{1+x^2}}\)

Einschub:

\(h(x)= \frac{1}{1+x^2} \)

\(h´(x)= \frac{0*(1+x^2)-1*2x}{(1+x^2)^2}=-\frac{2x}{(1+x^2)^2} \)

\(g´(x) =  − e^{\frac{1}{1+x^2}}*(-\frac{2x}{(1+x^2)^2})= e^{\frac{1}{1+x^2}}*\frac{2x}{(1+x^2)^2} \)

\( e^{\frac{1}{1+x^2}}*\frac{2x}{(1+x^2)^2}=0\)

\(x=0\)      \(g(0) = 1 − e^{\frac{1}{1}}=1-e\)

\(g´(x) = e^{\frac{1}{1+x^2}}*\frac{2x}{(1+x^2)^2} \)

\(g(-1) =1 − e^{\frac{1}{1+1}}=1-\sqrt{e} \)

\(g(-1) > g(0)\)??  →  \(1-\sqrt{e}>1-e \)→\(-\sqrt{e}>-e \)→\(\sqrt{e}<e \)✓

\( g(0)<g(1)\)?? → \(1-e<1-\sqrt{e} \)→ \(-e<-\sqrt{e} \)→ \(e>\sqrt{e} \)✓

\( \lim\limits_{x\to-\infty} 1 − e^{\frac{1}{1+x^2}}=0\) 

\( \lim\limits_{x\to\infty} 1 − e^{\frac{1}{1+x^2}}=0\)

Somit besitzt der Graph von \(f(x)\) ein Minimum ∈ ℝ.

Answer 5

\(g\) hat ein Minimum dort, wo \(e^{\frac{1}{1+x^2}}\) ein Maximum hat.

Nun ist die Exponentialfunktion streng monoton wachsend.

Sie nimmt also ihr Maximum dort an, wo \(\frac{1}{1+x^2}\)

sein Maximum annimmt, also der Kehrwert \(1+x^2\) sein Minimum hat,

was offenbar bei \(x=0\) der Fall ist.