Beschränke dich mal nicht auf die Strecke AB, sondern betrachte die Gerade AB.
Sie schneidet den Inversionskreis. Diese Schnittpunkte werden auf sich selbst abgebildet. Die Gerade geht in beiden Richtungen "ins Unendliche", sie wird durch die Abbildung deshalb zu einem Kreis, der durch den Mittelpunkt des Inversionskreises verläuft. durch diese drei Punkte ist das Abbild der Gerade AB schon eindeutig bestimmt.
Zusätzlich kannst du aber noch den Bildpunkt von E bestimmen. Da E von O den Abstand r/2 hat, hat E' von O den Abstand 2r.
Aber diesen Kreis hast du ja selbst gefunden.
Da die Gerade AD durch O geht, wird sie auf sich selbst abgebildet. Allerdings werden kreisinnere Punkte nach außen abgebildet und umgekehrt. Du kannst auch nicht sofort davon ausgehen, dass konkret A auf D und D auf A abgebildet würden (auch wenn sich das letztendlich als wahr herausstellt.
Fakt ist: Da A auf der Gerade AD und auf der Gerade AB liegt, liegt A' dort, wo sich die Bildgerade der Gerade AD (also letztendlich die Gerade AD selbst) und der Bildkreis der Gerade AB schneiden.
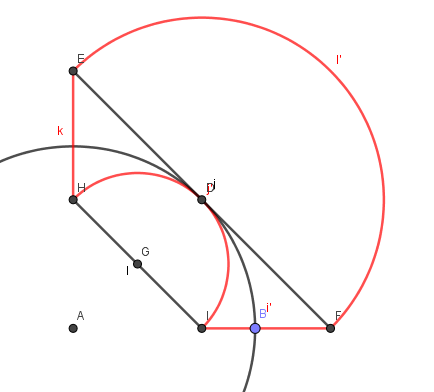
In der Abbildung siehst du rot das Bild des Trapezes. (Punktbezeichnungen entsprechen NICHT dem Original).