Aufgabe:
Wir betrachten \( \mathbb{R}^{4} \) mit Standardskalarprodukt. Verwenden Sie ohne Beweis, dass die untenstehende Menge \( B \) eine Basis von \( \mathbb{R}^{4} \) ist.
\( B:=\left\{b_{1}:=\left(\begin{array}{l} 1 \\ 1 \\ 1 \\ 1 \end{array}\right), \quad b_{2}:=\left(\begin{array}{c} 1 \\ -1 \\ 1 \\ -1 \end{array}\right), \quad b_{3}:=\left(\begin{array}{l} 0 \\ 1 \\ 1 \\ 0 \end{array}\right), \quad b_{4}:=\left(\begin{array}{c} 0 \\ 1 \\ 1 \\ -1 \end{array}\right)\right\} \)
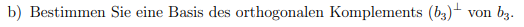
Problem/Ansatz
Hallo, benötige etwas Hilfe bei der obigen Aufgabe.
Ansatz: Da wir uns im R^4 befinden, besitzt das Komplement zu b3 einen 3-Dimensionalen Lösungsraum.
Also erhalten wir beim Lösen des Gleichungssystems 3 Parameter.
Daraus kann ich direkt 2 Orthogonale Vektoren erkennen, nämlich: (0,0,0,1) und (1,0,0,0)
Leider habe ich etwas Probleme um auf den letzten Orthogonalen Vektor zu kommen. Würde ich den Vektor wie oben bestimmen würde ich (0,1,0,0) erhalten, der nicht Orthogonal ist zu b3.
Würde mich über Hilfe freuen