Aufgabe:
Die Höhe einer wachsenden Pflanze wird beschrieben durch:
h (t)= -1/20(25+16t)e-0,64t+1,4
t>=0
Die 1. Ableitung hab ich in einer Teilaufgabe schon ausgerechnet:
h'(t)= 0,512×t×e-0,64t
Aufgabenstellung:
3. Begründen Sie kurz auf mathematischer Ebene: Die Höhe der Pflanze ist monoton zunehmend. Geben Sie die theoretische Maximalwert der Pflanze an. Begründen Sie Ihre Rechnung unter Zurückführung auf die Grenzwertregeln.
Problem/Ansatz:
Nur bei der Teilaufgabe 3 hab ich Probleme. Hab zwar schon einen Ansatz, aber ich glaube der ist falsch.
Könnte mir das jemand verbessern?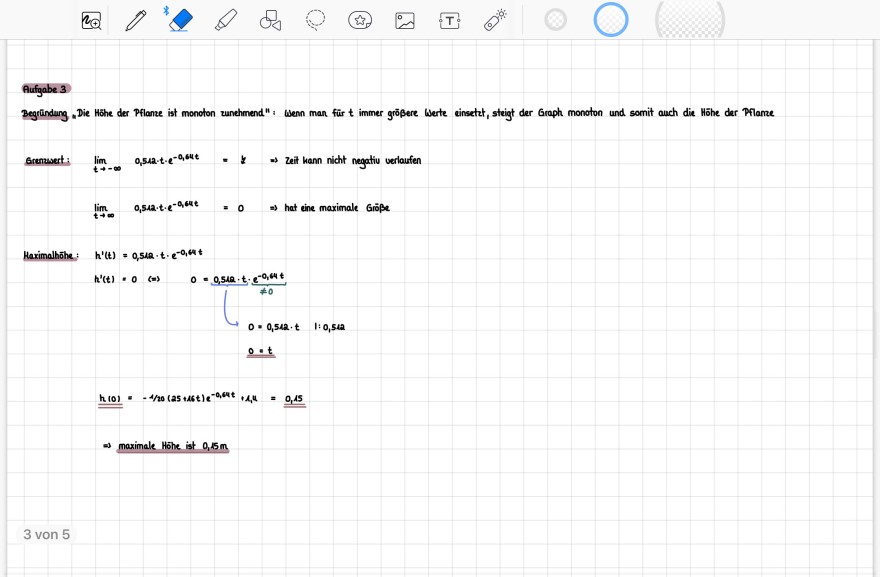
Text erkannt:
Aufgabe 3
Begründung. "Die Hohe der Pflanze ist monoton zunehmend"; Wenn man für \( t \) immer größere Werte einsetzt, steigt der Graph monoton und somit auch die Höhe der Pflame
Grenzwert: \( \lim \limits_{t \rightarrow-\infty} 0,542 \cdot t \cdot e^{-0,64 t}=y \Rightarrow \) zeit hann nicht negativ verlaufen
\( \lim \limits_{t \rightarrow \infty} 0,512 \cdot t \cdot e^{-0,64 t}=0 \Rightarrow \) hat eine maximale Größe
Haximalhöhe: \( \quad h^{\prime}(t)=0,542 \cdot t \cdot e^{-0,44 t} \)
\( \begin{array}{l} h^{\prime}(t)=0 \Leftrightarrow 0=\frac{0,512 \cdot t \cdot t \cdot e^{-0,64 t}}{\neq 0} \\ 0=0,542 \cdot t \quad 1: 0,512 \\ 0 \cdot t \\ \underline{\underline{h}(0)}=-1 / 20(25+16 t) e^{-0,64 t}+1,4=0,15 \\ \end{array} \)
\( \Rightarrow \) maximale Hohe ist \( 0,15 \mathrm{~m} \)
3 von 5