Aufgabe:
Die Abbildung 1 zeigt den Graph der Ableitungsfunktion der Funktion f(x)
a) Begründen Sie mit Hilfe des gegebenen Graphen der Ableitung f‘(x) folgende Aussagen:
Text erkannt:
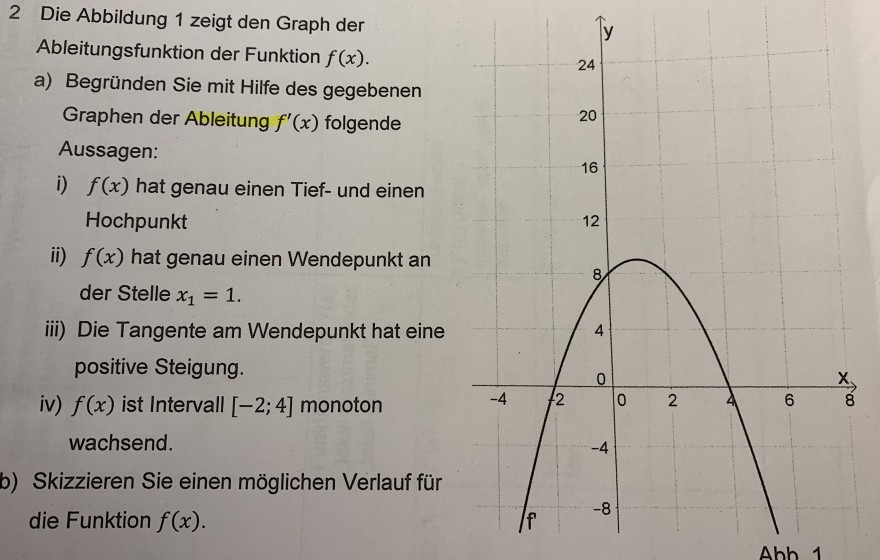
2 Die Abbildung 1 zeigt den Graph der
Ableitungsfunktion der Funktion \( f(x) \).
a) Begründen Sie mit Hilfe des gegebenen
Graphen der Ableitung \( f^{\prime}(x) \) folgende
Aussagen:
i) \( f(x) \) hat genau einen Tief- und einen
Hochpunkt
ii) \( f(x) \) hat genau einen Wendepunkt an der Stelle \( x_{1}=1 \).
iii) Die Tangente am Wendepunkt hat eine positive Steigung.
iv) \( f(x) \) ist Intervall \( [-2 ; 4] \) monoton wachsend.
b) Skizzieren Sie einen möglichen Verlauf für die Funktion f(x).
Problem/Ansatz:
Ich habe bei dieser Aufgabe Probleme und komme nicht weiter. Jedoch habe ich einige Ideen:
a) Hier würde ich sagen es gibt nur einen Hochpunkt (1|9)
b) den Wendepunkt würde ich auch am Hochpunkt ausmachen, weil sich dort der Verlauf der Funktion ändert
c) demnach würde die Steigung dort negativ sein, da der Graph fällt
Bei den anderen Aufgaben habe mich leider überhaupt keine Ahnung und würde mich über Hilfe beim Lösen der Aufgabe sehr freuen.