Taylorentwicklung eines Polynoms

Question

Aufgabe:

Ich soll das Taylorpolynom 5ter Ordnng zum Entwicklungspunkt 0 bestimmen.

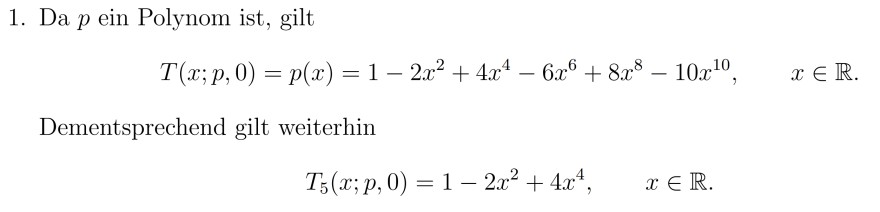
Text erkannt:

1. Da \( p \) ein Polynom ist, gilt
\( T(x ; p, 0)=p(x)=1-2 x^{2}+4 x^{4}-6 x^{6}+8 x^{8}-10 x^{10}, \quad x \in \mathbb{R} . \)
Dementsprechend gilt weiterhin
\( T_{5}(x ; p, 0)=1-2 x^{2}+4 x^{4}, \quad x \in \mathbb{R} . \)

Problem/Ansatz:

Ich frage mich nach der Formulierung der Lösung, ob es eine allgemeine Regel gibt, um die Taylorentwicklung eines Polynoms an diesem selbst direkt abzulesen? Hoffentlich wisst ihr mehr als ich. Danke schonmal für die Hilfe!

Answer 1

Ein Polynom ist seine eigene Taylorreihe mit Entwicklungspunkt

\(x_0=0\): \(p(x)=\sum_{k=0}^{\infty} a_kx^k\), wobei \(a_k\neq 0\)

nur für endlich viele \(k\) gilt. Das Taylorpolynom

um 0 n-ter Ordnung erhält man aus \(p\), indem man

nur die Glieder bis zur Potenz \(x^n\) hinschreibt.