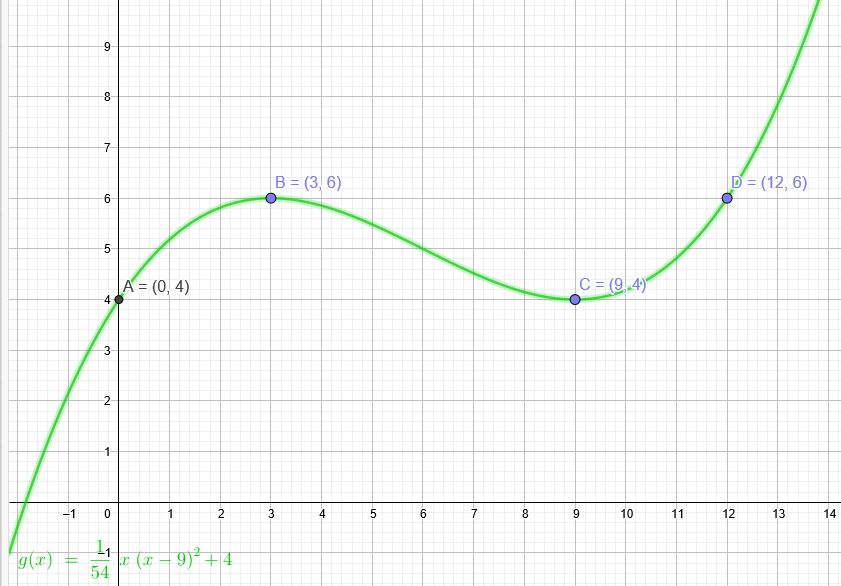
\(A(0|4) B(3|6) C(9|4) und D(12,6)\)
Ich verschiebe um 4 Einheiten nach unten:
\(A´(0|0) B´(3|2) C´(9|0) und D´(12,2)\)
\(f(x)=a*x*(x-9)^2\)
\(f(3)=a*3*(3-9)^2=a*3*(-6)^2=108a=2\) \(a=\frac{1}{54}\)
\(f(x)=\frac{1}{54}*x*(x-9)^2\)
Nun wieder 4 zurück nach oben:
\(p(x)=\frac{1}{54} *x*(x-9)^2+4 \)