Berechnen und bestimmen der Gewinnfunktion

Question

Aufgabe:

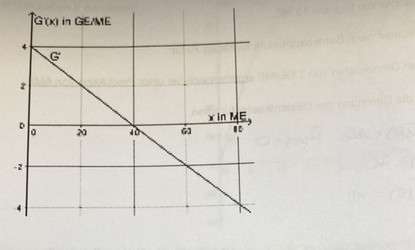
In dem Graph wird eine Grenzgewinnfunktion G' dargestellt.

a) Erstellen Sie die Gleichung der Grenzgewinnfunktion

b) Erklären Sie, wie Sie in der Grafik die Stelle des maximalen Gewinns able können.

c) Der maximale Gewinn beträgt 45 GE. Ermitteln Sie die Gleichung der Gewinnfunktion \( G \).

d) Lesen Sie an der Funktionsgleichung von G die Fixkosten der Kostenfu

Problem/Ansatz:

Kann mir jemand helfen?

Comments

Bei Aufgabe d) feh

Answer 1

a) Lies die Punkte (0|4) und (80| -4) ab und setze sie in die Punkt-Steigungs-Form ein: \( \frac{y-4}{x} \)=\( \frac{4+4}{-80} \)= - \( \frac{1}{10} \). Aufgelöst nach y: y= - \( \frac{1}{10} \)x+4.

Answer 2

b)  Gmax = Nullstelle von G'(x)

G'(x) = 0

x= 40 (ablesen)

oder:

-1/10*x+4 =0

-1/10*x = -4

x= -4*(-10) = 40

c) G'(x) integrieren:

G(x)= -1/20*x^2+4x +C

G(x) = 45

-1/20*40^2+4*40+C= 45

C= 1,4375

G(x) = -1/20*x^2+4x+1,4375

d) Fixkosten = 1,4375