Aufgabe:

Text erkannt:
Sei \( V_{4}=\{f \in \mathbb{R}[X] \mid \operatorname{grad}(f) \leq 4\} \) der \( \mathbb{R} \)-Vektorraum der Polynome vom Grad kleiner gleich 4.
Sei \( \phi: V_{4} \rightarrow V_{4} \) der Endomorphismus gegeben durch \( \phi\left(\sum \limits_{j=0}^{4} a_{i} X^{i}\right)=\sum \limits_{i=0}^{2} a_{2 i} X^{i} \).
Sei \( \mathcal{B}=\left\{1, x, x^{2}, x^{3}, x^{4}\right\} \) eine Basis von \( V_{4} \) und sei
\( \mathcal{B}^{\prime}=\left\{1,1+x, 1+x+x^{2}, 1+x+x^{2}+x^{3}, 1+x+x^{2}+x^{3}+x^{4}\right\} \)
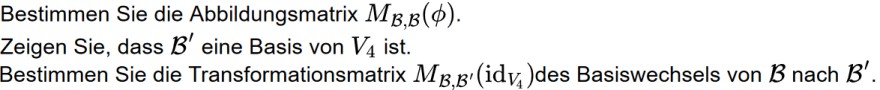
Text erkannt:
Bestimmen Sie die Abbildungsmatrix \( M_{\mathcal{B}, \mathcal{B}}(\phi) \)
Zeigen Sie, dass \( \mathcal{B}^{\prime} \) eine Basis von \( V_{4} \) ist.
Bestimmen Sie die Transformationsmatrix \( M_{\mathcal{B}^{\mathcal{B}^{\prime}}}\left(\mathrm{id}_{V_{4}}\right) \) des Basiswechsels von \( \mathcal{B} \) nach \( \mathcal{B}^{\prime} \).
Problem/Ansatz: Ich weiß, leider nicht wie ich hier vorgehen soll. Anhand von Matrixen und Basen von Matrizen, kann ich eine Transformationsmatrix von Basis A zu Basis B bilden, wie macht man das bei Polynomen?